Advanced Data Structure
B-Tree
B-trees are balanced search trees designed to work well on disks or other directaccess secondary storage devices. B-trees are similar to red-black trees, but they are better at minimizing disk I/O operations. Many database systems use B-trees, or variants of B-trees, to store information.
B-trees differ from red-black trees in that B-tree nodes may have many children, from a few to thousands. That is, the “branching factor” of a B-tree can be quite large, although it usually depends on characteristics of the disk unit used. B-trees are similar to red-black trees in that every n-node B-tree has height O.lg n/. The exact height of a B-tree can be considerably less than that of a red-black tree, however, because its branching factor, and hence the base of the logarithm that expresses its height, can be much larger. Therefore, we can also use B-trees to implement many dynamic-set operations in time O(lgn).
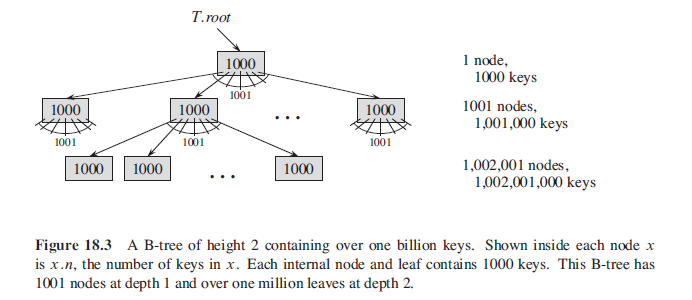
Definition of B-trees
minimum degree t
-
Every node other than the root must have at least t - 1 keys. Every internal node other than the root thus has at least t children. If the tree is nonempty, the root must have at least one key.
-
Every node may contain at most 2t - 1 keys. Therefore, an internal node may have at most 2t children. We say that a node is full if it contains exactly 2t - 1 keys.
Basic operations on B-trees
Searching a B-Tree

Insertion
Before we can insert, we need to know how to split a full node:
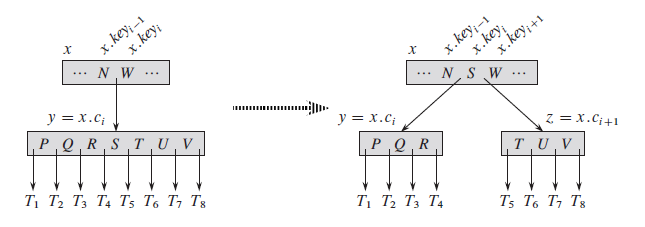


Deletion
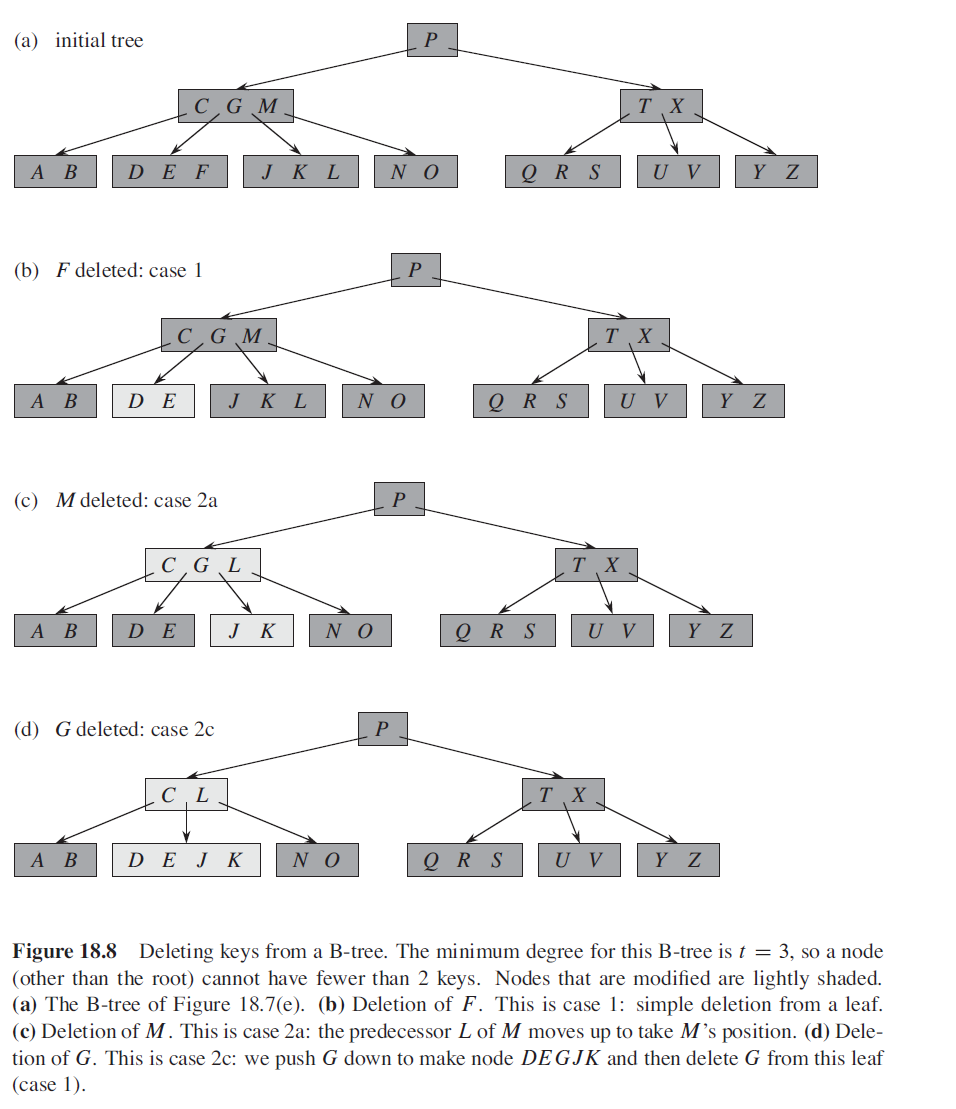

There are so many cases:



