Graph Algorithms
Elementary Graph Algorithms
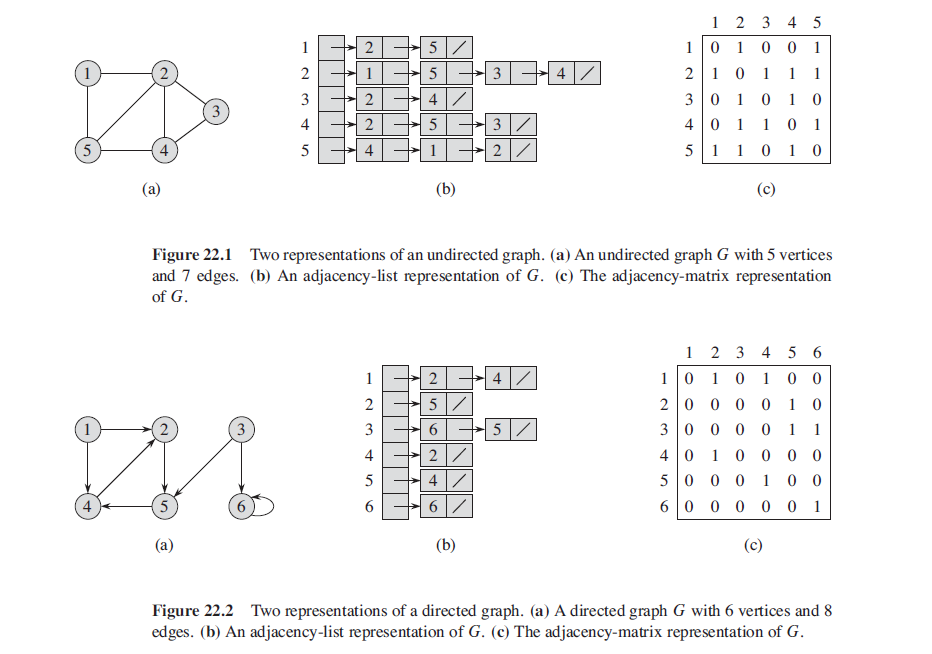
Representations of graphs
There are two ways to represent a graph:
Breadth-first search
Breadth-first search is one of the simplest algorithms for searching a graph and the archetype for many important graph algorithms. Given a graph G D .V;E/ and a distinguished source vertex s, breadth-first search systematically explores the edges of G to “discover” every vertex that is reachable from s. It computes the distance (smallest number of edges) from s to each reachable vertex. It also produces a “breadth-first tree” with root s that contains all reachable vertices.

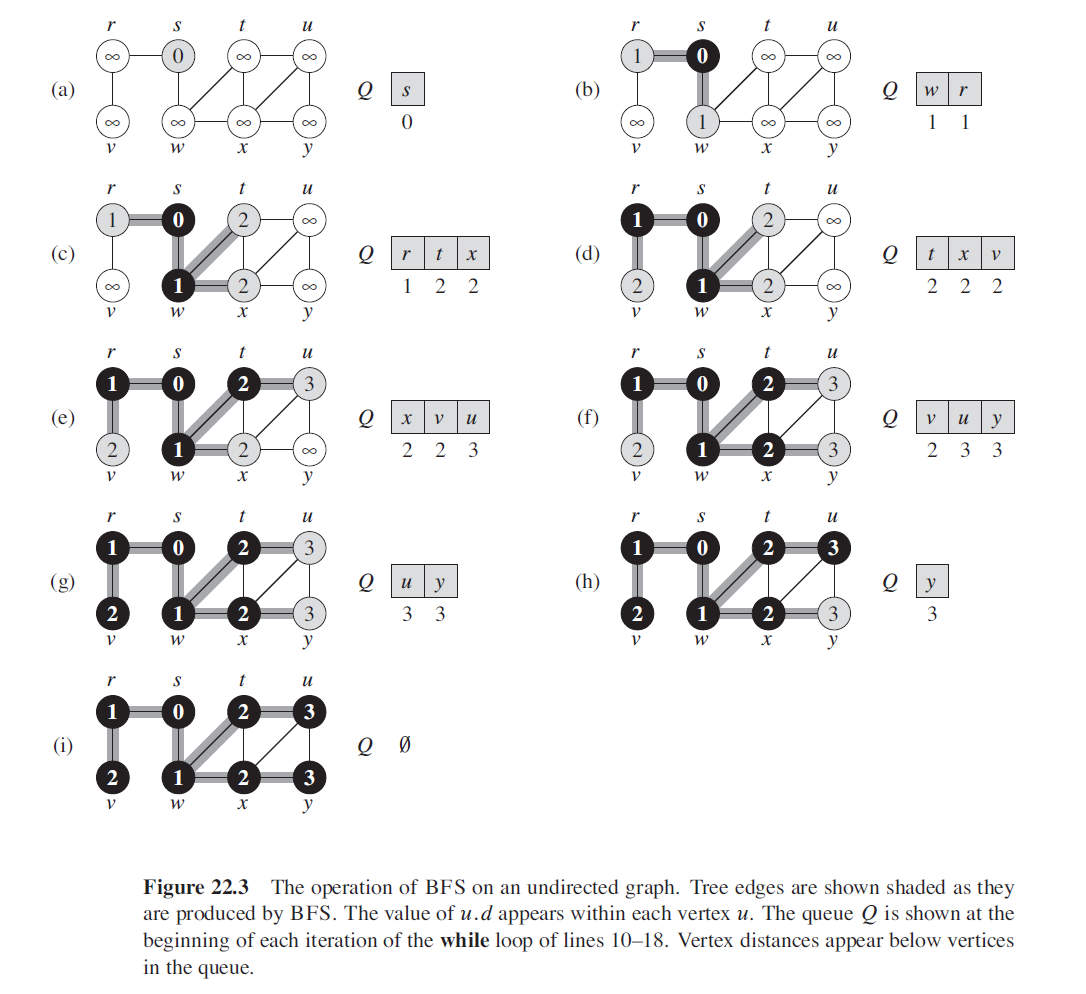
BFS can also find the shortest path from two vertexs.
The proof is complicated so skip, all I have to know is BSF can help you print shortest path from two vertex if you build your BFS tree by marking the parents of the vertex.
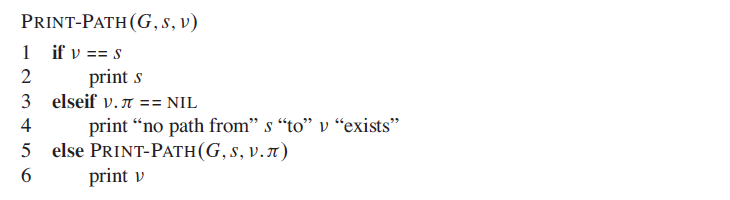
Depth-first search
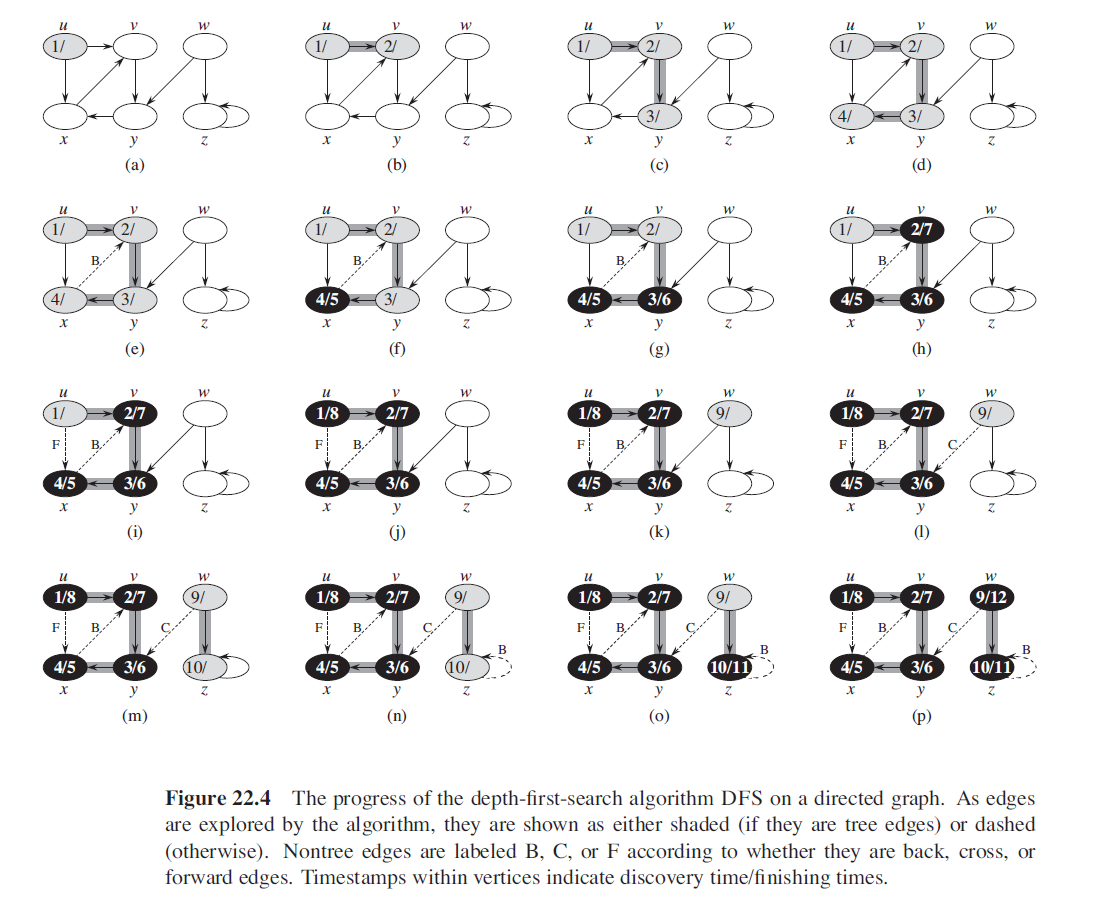
As in breadth-first search, depth-first search colors vertices during the search to indicate their state. Each vertex is initially white, is grayed when it is discovered in the search, and is blackened when it is finished, that is, when its adjacency list has been examined completely. This technique guarantees that each vertex ends up in exactly one depth-first tree, so that these trees are disjoint.
Besides creating a depth-first forest, depth-first search also timestamps each vertex. Each vertex v has two timestamps: the first timestamp v.d records when v is first discovered (and grayed), and the second timestamp v.f records when the search finishes examining v’s adjacency list (and blackens v). These timestamps provide important information about the structure of the graph and are generally helpful in reasoning about the behavior of depth-first search.



Topological sort
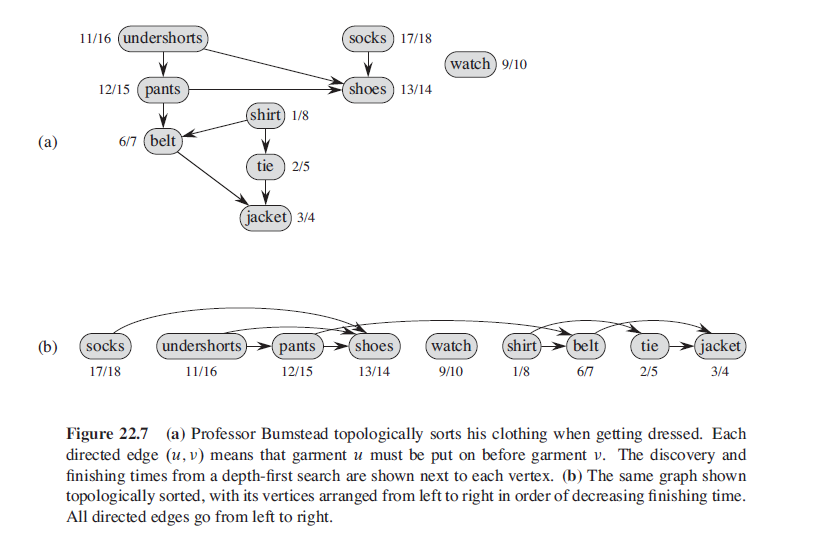
Many applications use directed acyclic graphs to indicate precedences among events. Figure 22.7 gives an example that arises when Professor Bumstead gets dressed in the morning. The professor must don certain garments before others (e.g., socks before shoes). Other items may be put on in any order (e.g., socks and pants). A directed edge (u,v) in the dag of Figure 22.7(a) indicates that garment u must be donned before garment v. A topological sort of this dag therefore gives an order for getting dressed. Figure 22.7(b) shows the topologically sorted dag as an ordering of vertices along a horizontal line such that all directed edges go from left to right.
TOPOLOGICAL-SORT(G)
1 call DFS(G) to compute finishing times v.f for each vertex v
2 as each vertex is finished, insert it onto the front of a linked list
3 return the linked list of vertices
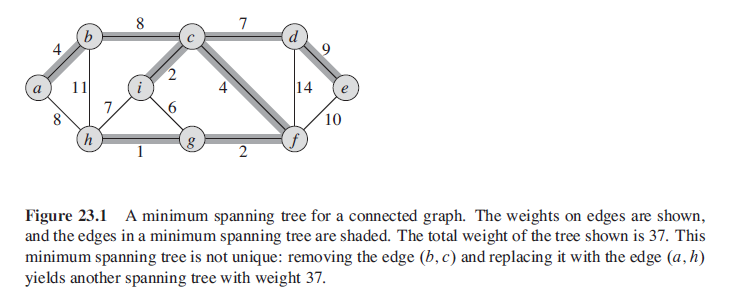
Minimum Spanning Trees
There are two ways to create the MST, also they yeild different operation, they will eventually find the same result and also, thay are both greedy algorithm.
Kruskal’s algorithm

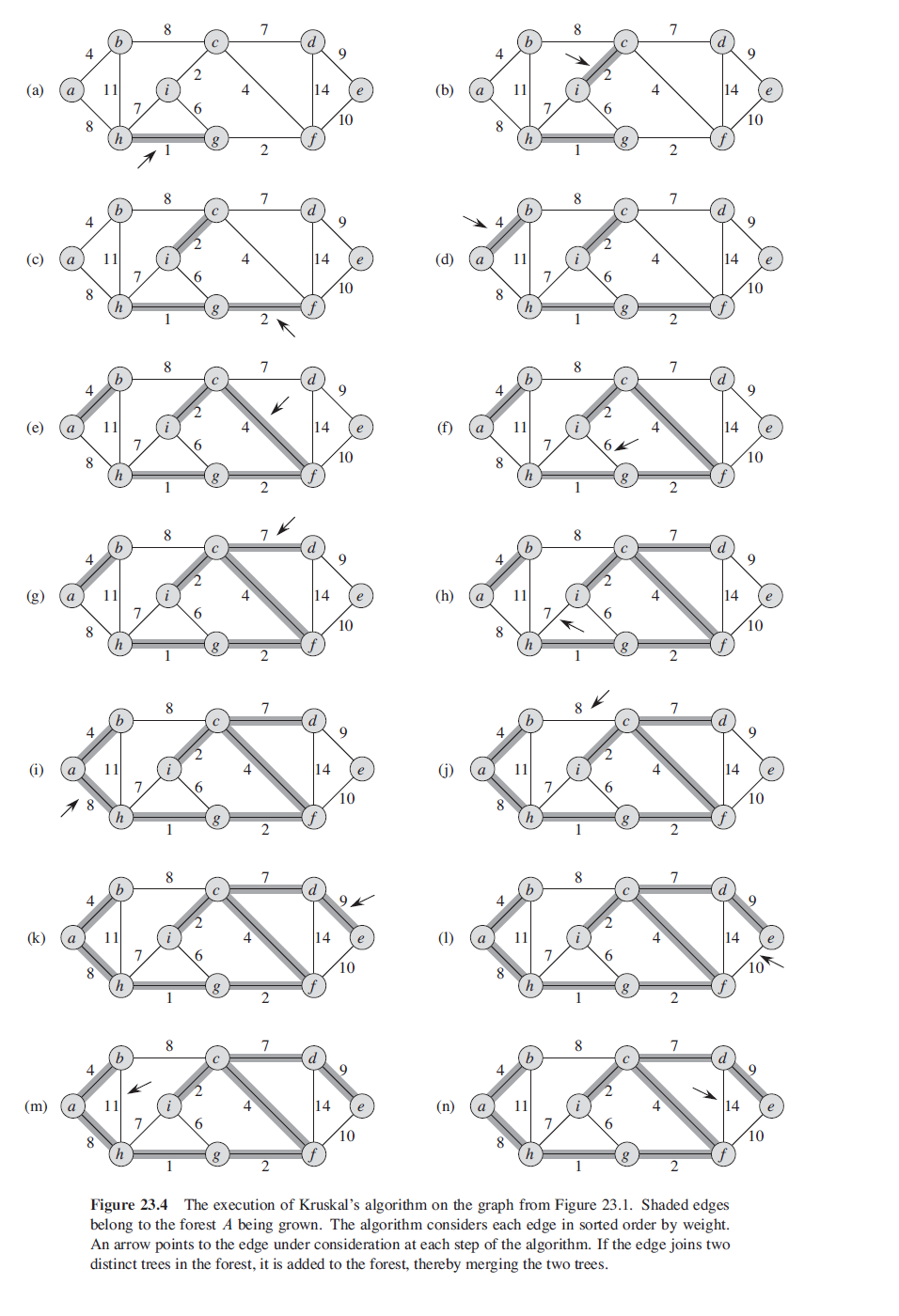
The main idea of Kruskal is that we put all of the edge into a priority queue based on edges’ weight, also we maintain a union set for cyclic checking and a result set. And for each time we pop the minimum edge, we first check whether it create a loop, if not, we can safely put it into our result and also, unionset for furthur checking.
Prim’s algorithm
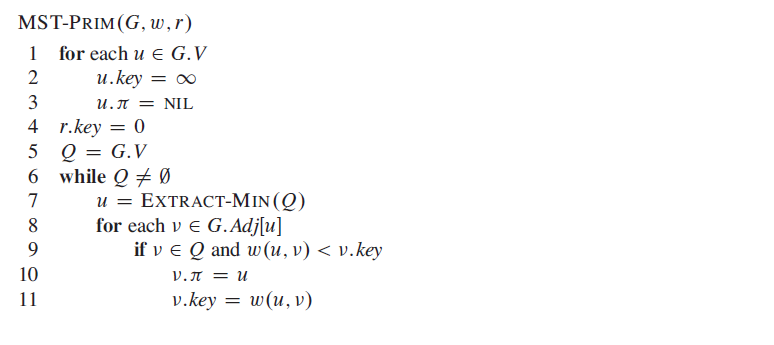
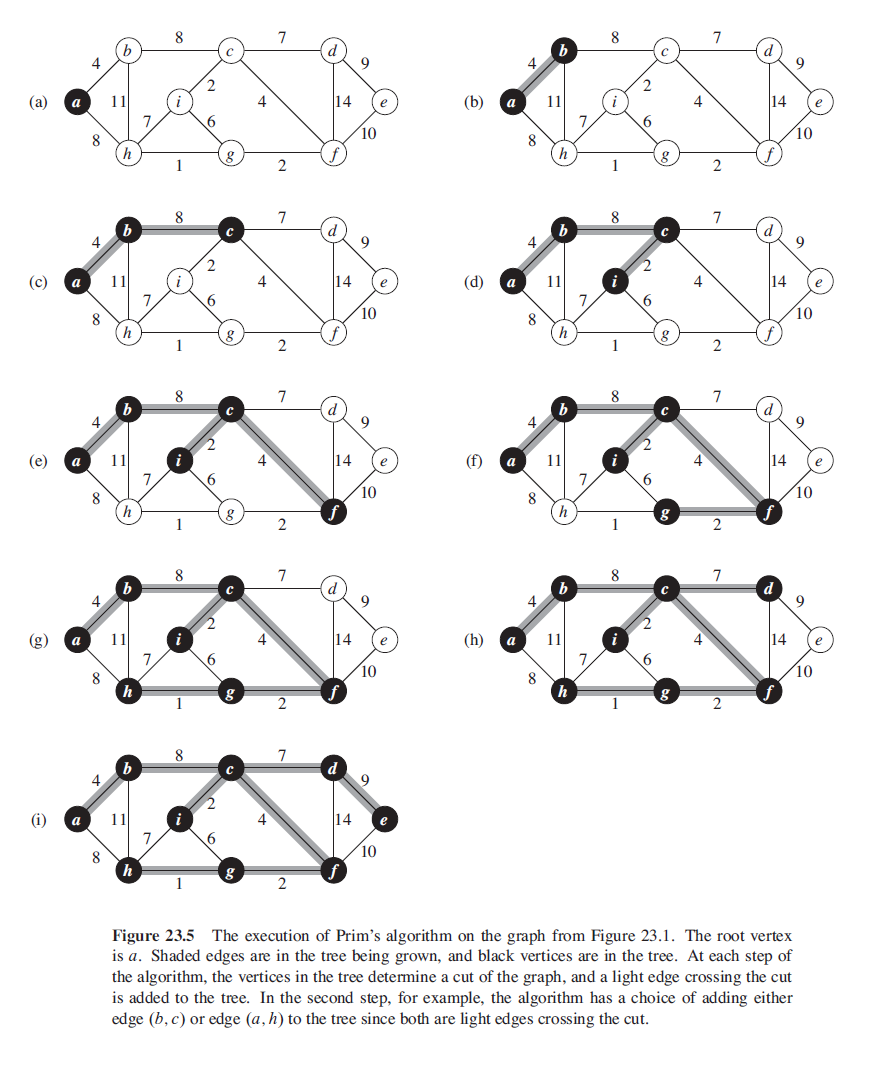
The prim working in a way that we keep an priority queue about the vertex based on their key. First we set all vertexs’ key to Infinite, and start arbitrarily. Then for each vertex, we exam all of its adjacenct vertexs and update their key with rule that if the edge weight is smaller than the key, then we update the vertex’s key, otherwise just keep it.
Then we just move to next step and extract vertex with the minimum key. Since we start with all the vertexs’ key with infinite, it’s clear that we always choose the vertex adjacent to explored vertexs.]
Shortest Paths
First we define the Relax operation:
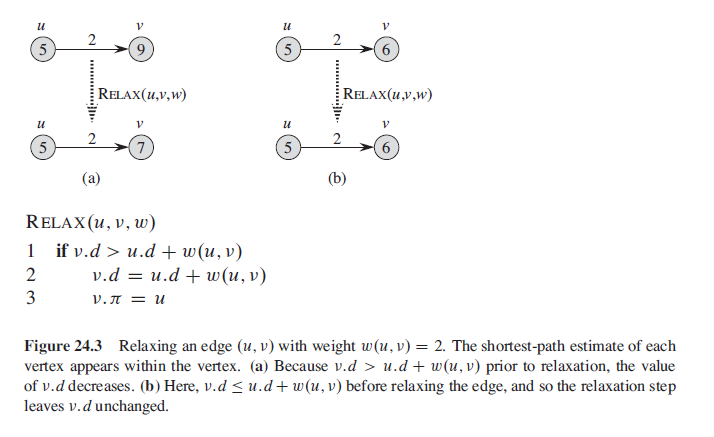
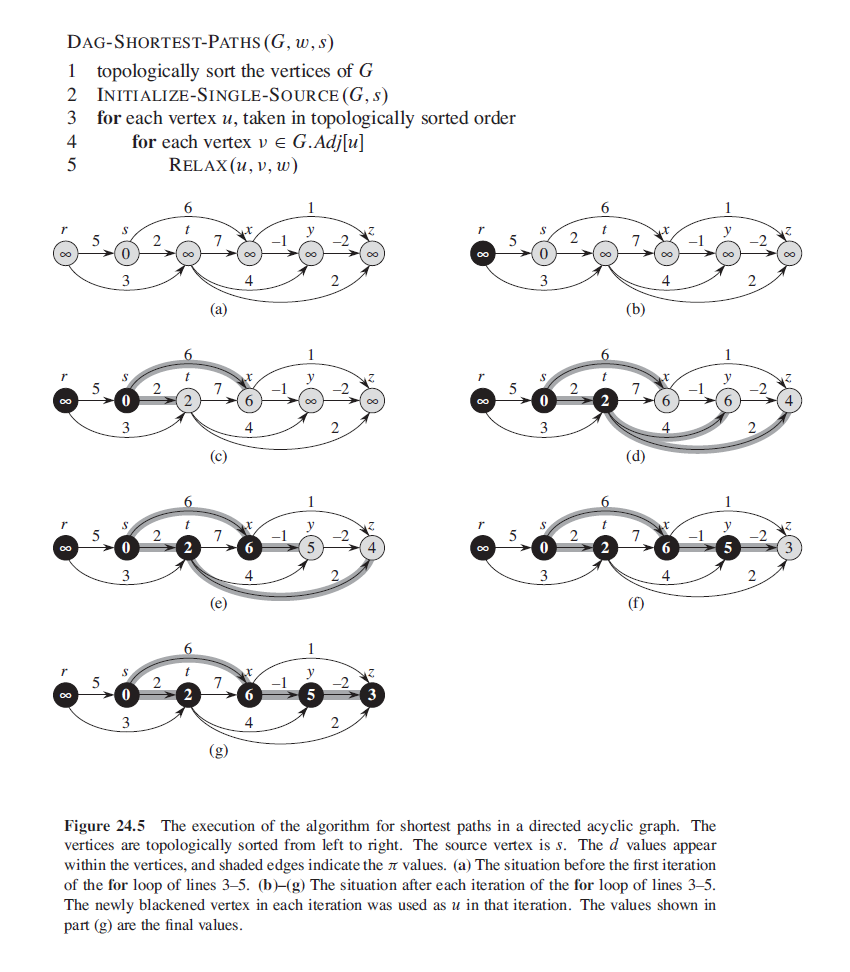
Single-source shortest paths in directed acyclic graphs
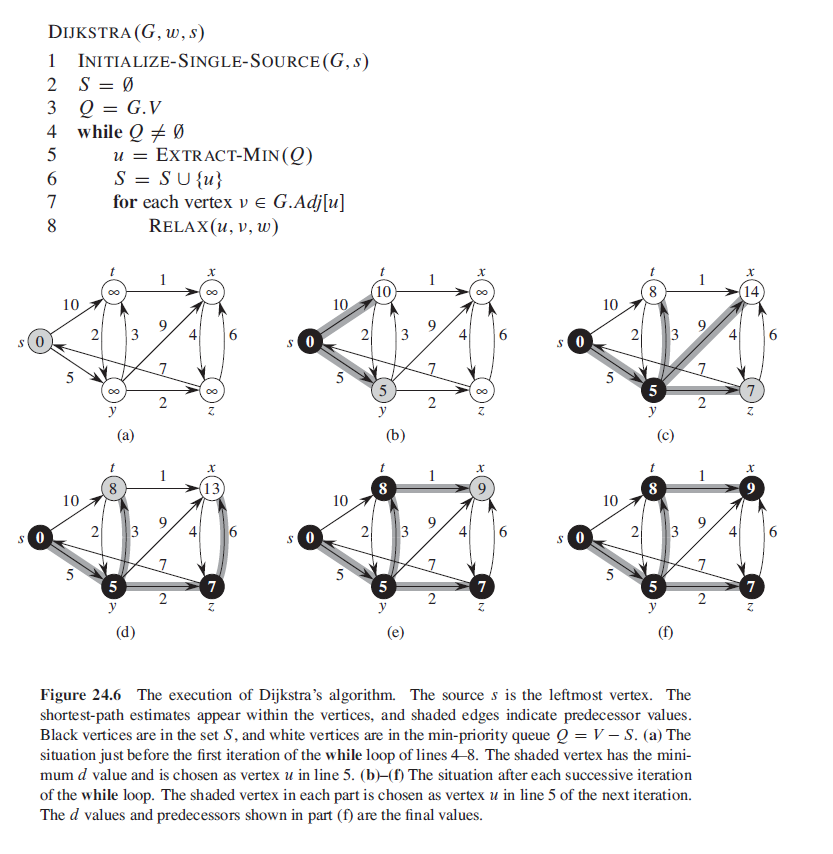
Dijkstra’s algorithm