- 2020-03-04
- 2020-03-05
- 2020-03-06
- 2020-03-07
- 2020-03-09
- 2020-03-10
- 2020-03-11
- 2020-03-12
- 2020-03-13
- 2020-03-17
- 2020-03-20
- 2020-03-22
- 2020-03-26
- 2020-03-27
- 2020-03-28
- 2020-03-29
- 2020-03-30
2020-03-04
835. Image Overlap
Description
Two images A and B are given, represented as binary, square matrices of the same size. (A binary matrix has only 0s and 1s as values.)
We translate one image however we choose (sliding it left, right, up, or down any number of units), and place it on top of the other image. After, the overlap of this translation is the number of positions that have a 1 in both images.
(Note also that a translation does not include any kind of rotation.)
What is the largest possible overlap?
Example 1:
Input: A = [[1,1,0],
[0,1,0],
[0,1,0]]
B = [[0,0,0],
[0,1,1],
[0,0,1]]
Output: 3
Explanation: We slide A to right by 1 unit and down by 1 unit.
Notes:
1 <= A.length = A[0].length = B.length = B[0].length <= 30
0 <= A[i][j], B[i][j] <= 1
Solution
//use (i/N)*100+i%N to log the position, if i-j has the same value, means they are in the same shift.
class Solution {
public int largestOverlap(int[][] A, int[][] B) {
int N = A.length;
List<Integer> LA =new ArrayList(), LB = new ArrayList();
HashMap<Integer,Integer> count = new HashMap();
for(int i = 0; i<N*N;i++){
if(A[i/N][i%N]==1){
LA.add((i/N)*100+i%N);
}
}
for(int i = 0; i<N*N;i++){
if(B[i/N][i%N]==1){
LB.add((i/N)*100+i%N);
}
}
for(int i : LA){
for(int j : LB){
count.put(i-j, count.getOrDefault(i-j,0)+1);
}
}
int res = 0;
for(int i:count.values()){
res = Math.max(res, i);
}
return res;
}
}
2020-03-05
951. Flip Equivalent Binary Trees
Description
For a binary tree T, we can define a flip operation as follows: choose any node, and swap the left and right child subtrees.
A binary tree X is flip equivalent to a binary tree Y if and only if we can make X equal to Y after some number of flip operations.
Write a function that determines whether two binary trees are flip equivalent. The trees are given by root nodes root1 and root2.
Example 1:
Input: root1 = [1,2,3,4,5,6,null,null,null,7,8], root2 = [1,3,2,null,6,4,5,null,null,null,null,8,7]
Output: true
Explanation: We flipped at nodes with values 1, 3, and 5.
Flipped Trees Diagram
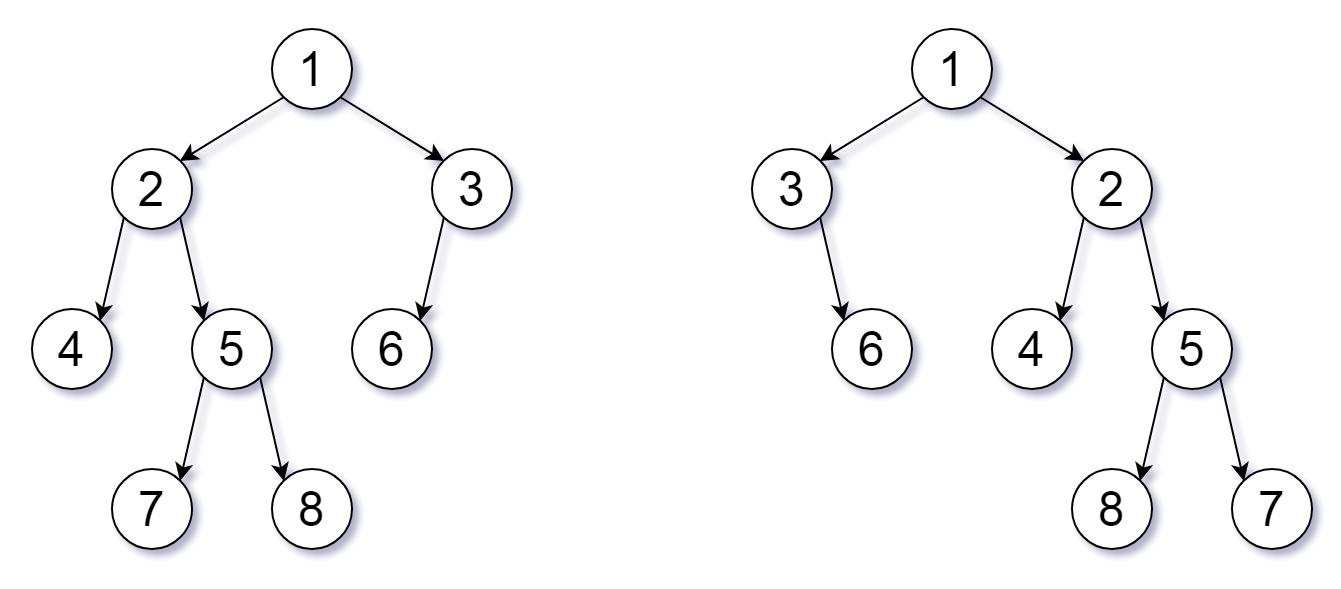
Note:
Each tree will have at most 100 nodes.
Each value in each tree will be a unique integer in the range [0, 99].
Solution
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public boolean flipEquiv(TreeNode root1, TreeNode root2) {
if(root1==null || root2 == null) return root1==root2;
return root1.val==root2.val &&( (flipEquiv(root1.left,root2.right) && flipEquiv(root1.right, root2.left)) || (flipEquiv(root1.left,root2.left) && flipEquiv(root1.right, root2.right)) );
}
}
public boolean flipEquiv(TreeNode root1, TreeNode root2) {
Queue<TreeNode> q1 = new LinkedList<>(), q2 = new LinkedList<>();
q1.offer(root1);
q2.offer(root2);
while (!q1.isEmpty() && !q2.isEmpty()) {
TreeNode n1 = q1.poll(), n2 = q2.poll();
if (n1 == null || n2 == null) {
if (n1 != n2) return false;
else continue;
}
if (n1.val != n2.val) {
return false;
}
if (n1.left == n2.left || n1.left != null && n2.left != null && n1.left.val == n2.left.val) {
q1.addAll(Arrays.asList(n1.left, n1.right));
}else {
q1.addAll(Arrays.asList(n1.right, n1.left));
}
q2.addAll(Arrays.asList(n2.left, n2.right));
}
return q1.isEmpty() && q2.isEmpty();
}
946. Validate Stack Sequences
Description
Given two sequences pushed and popped with distinct values, return true if and only if this could have been the result of a sequence of push and pop operations on an initially empty stack.
Example 1:
Input: pushed = [1,2,3,4,5], popped = [4,5,3,2,1]
Output: true
Explanation: We might do the following sequence:
push(1), push(2), push(3), push(4), pop() -> 4,
push(5), pop() -> 5, pop() -> 3, pop() -> 2, pop() -> 1
Example 2:
Input: pushed = [1,2,3,4,5], popped = [4,3,5,1,2]
Output: false
Explanation: 1 cannot be popped before 2.
Note:
0 <= pushed.length == popped.length <= 1000
0 <= pushed[i], popped[i] < 1000
pushed is a permutation of popped.
pushed and popped have distinct values.
Solution
class Solution {
//check every time pushed, and pop as much as possible.
//after pushed all items, try to pop evrything.
//check if all item in pushed and poped are used, which means nothing left in the stack.
public boolean validateStackSequences(int[] pushed, int[] popped) {
Stack<Integer> stack = new Stack();
int i = 0,j=0;
int pushLen = pushed.length, popLen = popped.length;
while(i<pushLen && j<popLen){
stack.push(pushed[i++]);
while(j<popLen && !stack.isEmpty() && stack.peek()==popped[j]){
stack.pop();
j++;
}
}
while(j<popLen && !stack.isEmpty() && stack.peek()==popped[j]){
stack.pop();
j++;
}
return i==pushLen && j==popLen;
}
}
41. First Missing Positive
Description
Given an unsorted integer array, find the smallest missing positive integer.
Example 1:
Input: [1,2,0]
Output: 3
Example 2:
Input: [3,4,-1,1]
Output: 2
Example 3:
Input: [7,8,9,11,12]
Output: 1
Note:
Your algorithm should run in O(n) time and uses constant extra space.
Solution
class Solution {
public int firstMissingPositive(int[] nums) {
int n = nums.length;
//remove all number that's invalid.
//only need number within range [1,n].
for(int i = 0;i<n;i++){
if(nums[i]<0 || nums[i]>n){
nums[i] = 0;
}
}
//since our possible numbers are in range [1,n], we can use mode n+1 to store the count information.
//so number i will add (n+1) to nums[i-1].
for(int i = 0;i<n;i++){
if(nums[i]%(n+1)==0) continue;
nums[nums[i]%(n+1)-1]+=(n+1);
}
//the first time we meet nums[i]/(n+1)==0 means this number has never been met before. return it.
for(int i = 0;i<n;i++){
if(nums[i]/(n+1)==0){
return i+1;
}
}
return n+1;
}
}
234. Palindrome Linked List
Description
Given a singly linked list, determine if it is a palindrome.
Example 1:
Input: 1->2
Output: false
Example 2:
Input: 1->2->2->1
Output: true
Follow up:
Could you do it in O(n) time and O(1) space?
Solution
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
//main idea is to reverse the second half and compare two linkedlist.
class Solution {
public boolean isPalindrome(ListNode head) {
ListNode fast = head, slow = head;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
}
//if count is odd, then slow is now the middle one, move to next.
if (fast != null) {
slow = slow.next;
}
slow = reverse(slow);
fast = head;
//fast can only be equal or one longer than slow, so only need to take care of the slow.
while (slow != null) {
if (fast.val != slow.val) {
return false;
}
fast = fast.next;
slow = slow.next;
}
return true;
}
public ListNode reverse(ListNode head) {
if(head == null){
return null;
}
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode pre = dummy;
ListNode cur = dummy.next;
ListNode than = cur.next;
while(than != null){
cur.next = than.next;
than.next = pre.next;
pre.next = than;
than = cur.next;
}
return dummy.next;
}
}
2020-03-06
18. 4Sum
Description
Given an array nums of n integers and an integer target, are there elements a, b, c, and d in nums such that a + b + c + d = target? Find all unique quadruplets in the array which gives the sum of target.
Note:
The solution set must not contain duplicate quadruplets.
Example:
Given array nums = [1, 0, -1, 0, -2, 2], and target = 0.
A solution set is:
[
[-1, 0, 0, 1],
[-2, -1, 1, 2],
[-2, 0, 0, 2]
]
Solution
//main idea is to use recursion to change a k-sum problem to k-1-sum problem which end with 2-sum and using 2pointer to solve.
//4 sum, can be solved by taking a number, and solve 3-sum for the rest of the array.
class Solution {
int len = 0;
public List<List<Integer>> fourSum(int[] nums, int target) {
len = nums.length;
Arrays.sort(nums);
return kSum(nums,target,4,0);
}
public List<List<Integer>> kSum(int[] nums, int target, int k, int index){
ArrayList<List<Integer>> res= new ArrayList();
if(index >= len){
return res;
}
if(k==2){
int i = index, j = len-1;
while(i<j){
if(nums[i] + nums[j] == target){
List<Integer> temp = new ArrayList();
temp.add(nums[i]);
temp.add(nums[j]);
res.add(temp);
while(i<j && nums[i]==nums[i+1]){
i++;
}
while(i<j && nums[j]==nums[j-1]){
j--;
}
i++;
j--;
}else if(nums[i] + nums[j] < target){
i++;
}else{
j--;
}
}
}else{
for(int i = index;i<len-k+1;i++){
List<List<Integer>> temp= kSum(nums,target-nums[i],k-1,i+1);
if(temp != null){
for(List<Integer> l : temp){
l.add(nums[i]);
res.add(l);
}
}
while(i<len-k+1 && nums[i]==nums[i+1]){
i++;
}
}
}
return res;
}
}
84. Largest Rectangle in Histogram
Description
Given n non-negative integers representing the histogram’s bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

The largest rectangle is shown in the shaded area, which has area = 10 unit.
Example:
Input: [2,1,5,6,2,3]
Output: 10
Solution
//main idea is whenever the current height is lower than previous one, keep popup all previous height that's larger than cur.
//so we can sure that in the current stack, heights are ascending.
//so for position i, we can say i-1 is the max one. and we can use this max to count all previous value.
//for example, 215562, when at the end 2, 6 is the previous max, so i-s.peek()-1 will the the length which is 1.
//then we can say 5 is the next one, and i-s.peek()-1 will be 2, since 6 was poped out, and now the area is 5*2.
//then as second 5 poped out, we know i-s.peek()-1 is 3, and height is still 5, so area is 15.
//next we meet 1 which is smaller than i, so we don't pop.
//now in the stack is 1,2 , also ascending.
//need to take care the last element i = len.
class Solution {
public int largestRectangleArea(int[] heights) {
if(heights==null || heights.length==0) return 0;
Stack<Integer> s = new Stack();
int len = heights.length;
int res = 0;
for(int i=0;i<len;i++){
while(!s.isEmpty() && heights[s.peek()] > heights[i]){
int mostLeft = s.pop();
res = Math.max(res,heights[mostLeft] * (s.isEmpty()?i:i-s.peek()-1));
}
s.push(i);
}
while(!s.isEmpty()){
int mostLeft = s.pop();
res = Math.max(res,heights[mostLeft] * (s.isEmpty()?len:len-s.peek()-1));
}
return res;
}
}
85. Maximal Rectangle
Hard
2157
59
Add to List
Share Given a 2D binary matrix filled with 0’s and 1’s, find the largest rectangle containing only 1’s and return its area.
Example:
Input:
{
{"1","0","1","0","0"},
{"1","0","1","1","1"},
{"1","1","1","1","1"},
{"1","0","0","1","0"}
}
Output: 6
Solution
//same idea as previous, except we keep a list h which present the max height for each col.
class Solution {
public int maximalRectangle(char[][] matrix) {
if(matrix==null || matrix.length==0 || matrix[0].length==0) return 0;
int rLen = matrix.length;
int cLen = matrix[0].length;
int[] h = new int[cLen+1];
int res = 0;
for(int r=0; r<rLen;r++){
Stack<Integer> s = new Stack();
for(int i = 0;i<=cLen;i++){
//maintain a list of height represent the current max height for each col.
if(i<cLen){
if(matrix[r][i]=='1') h[i]+=1;
else h[i] = 0;
}
while(!s.isEmpty() && h[i]<h[s.peek()]){
int left = s.pop();
res = Math.max(res, h[left]*(s.isEmpty()?i:i-s.peek()-1));
}
s.push(i);
}
}
return res;
}
}
2020-03-07
1192. Critical Connections in a Network
Description
There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.
A critical connection is a connection that, if removed, will make some server unable to reach some other server.
Return all critical connections in the network in any order.
Example 1:
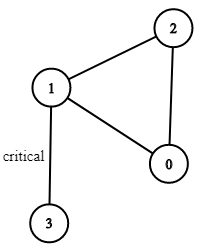
Input: n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
Output: [[1,3]]
Explanation: [[3,1]] is also accepted.
Constraints:
1 <= n <= 10^5
n-1 <= connections.length <= 10^5
connections[i][0] != connections[i][1]
There are no repeated connections.
Solution
import java.util.*;
class Solution {
int timer;
public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
List<Integer>[] graph = new ArrayList[n];
for (int i = 0; i < n; i++) graph[i] = new ArrayList<>();
//build graph.
for (List<Integer> oneConnection : connections) {
graph[oneConnection.get(0)].add(oneConnection.get(1));
graph[oneConnection.get(1)].add(oneConnection.get(0));
}
//set timer to 1 so in timeStampNode if val = 0 means unvisited.
timer = 1;
List<List<Integer>> res = new ArrayList<>();
int[] timeStampAtNode = new int[n];
connectionUtil(graph, -1, 0, timeStampAtNode, res);
return res;
}
public void connectionUtil(List<Integer>[] graph, int parent, int node, int[] timeStampAtNode, List<List<Integer>> res) {
//record the current time to this node.
timeStampAtNode[node] = timer++;
int curTime = timeStampAtNode[node];
for (int next : graph[node]) {
//prevent trace back to parent as it's undirected grapgh.
if (next == parent) continue;
//if child has not been visited.
if (timeStampAtNode[next] == 0) {
connectionUtil(graph, node, next, timeStampAtNode, res);
}
//child are supposed to be visited later, but if it has a smaller timestamp, means a circle.
//how? by maintains the min value of the timestamp.
//so all item on the same loop will have the same timestamp as min.
timeStampAtNode[node] = Math.min(timeStampAtNode[node], timeStampAtNode[next]);
//if curTime is strictly smaller than child, means this vertex is critical.
if (curTime < timeStampAtNode[next]) {
res.add(Arrays.asList(node, next));
}
}
}
}
128. Longest Consecutive Sequence
Description
Given an unsorted array of integers, find the length of the longest consecutive elements sequence.
Your algorithm should run in O(n) complexity.
Example:
Input: [100, 4, 200, 1, 3, 2]
Output: 4
Explanation: The longest consecutive elements sequence is [1, 2, 3, 4]. Therefore its length is 4.
Solution
//main idea is to use HashSet to store all values and check next num is exist.
//why it's O(n): by using the trick by checking whether x-1 exist in the set, we can only iterate through the sequence once, only when this number is the start of this sequence.
//so all number will only be iterate through once.
class Solution {
public int longestConsecutive(int[] nums) {
HashSet<Integer> set = new HashSet<Integer>();
for(int n: nums){
set.add(n);
}
int res = 0;
for(int x : nums){
if(!set.contains(x-1)){
int y = x;
while(set.contains(y)){
y++;
}
res = Math.max(res, y-x);
}
}
return res;
}
}
118. Pascal’s Triangle
Description
Given a non-negative integer numRows, generate the first numRows of Pascal’s triangle.
In Pascal’s triangle, each number is the sum of the two numbers directly above it.
Example:
Input: 5
Output:
[
[1],
[1,1],
[1,2,1],
[1,3,3,1],
[1,4,6,4,1]
]
Solution
//no need to handle special case for 1 and 2.
//use index ==0 and == last to insert 1.
class Solution {
public List<List<Integer>> generate(int numRows) {
List<List<Integer>> res = new ArrayList();
if(numRows<=0) return res;
for(int i = 0;i<numRows;i++){
List<Integer> row = new ArrayList();
for(int j = 0; j< i+1;j++){
//will handle special case where i = 0/1 (height 1/2) .
if(j==0 || j==i){
row.add(1);
}else{
//when i==0, it will not go into here.
row.add(res.get(i-1).get(j-1)+res.get(i-1).get(j));
}
}
res.add(new ArrayList(row));
}
return res;
}
}
442. Find All Duplicates in an Array
Description
Given an array of integers, 1 ≤ a[i] ≤ n (n = size of array), some elements appear twice and others appear once.
Find all the elements that appear twice in this array.
Could you do it without extra space and in O(n) runtime?
Example:
Input:
[4,3,2,7,8,2,3,1]
Output:
[2,3]
Solution
//same idea, if we have number from 1 to n, we can use (n+1) as mode and record a number by adding (n+1)
class Solution {
public List<Integer> findDuplicates(int[] nums) {
int n = nums.length;
for(int i = 0;i<n;i++){
nums[(nums[i]%(n+1))-1] += (n+1);
}
List<Integer> res = new ArrayList();
for(int i = 0;i<n;i++){
if(nums[i]/(n+1)==2) res.add(i+1);
}
return res;
}
}
312. Burst Balloons
Description
Given n balloons, indexed from 0 to n-1. Each balloon is painted with a number on it represented by array nums. You are asked to burst all the balloons. If the you burst balloon i you will get nums[left] * nums[i] * nums[right] coins. Here left and right are adjacent indices of i. After the burst, the left and right then becomes adjacent.
Find the maximum coins you can collect by bursting the balloons wisely.
Note:
You may imagine nums[-1] = nums[n] = 1. They are not real therefore you can not burst them.
0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100
Example:
Input: [3,1,5,8]
Output: 167
Explanation: nums = [3,1,5,8] --> [3,5,8] --> [3,8] --> [8] --> []
coins = 3*1*5 + 3*5*8 + 1*3*8 + 1*8*1 = 167
Solution
//For the first we have nums[i-1]*nums[i]*nums[i+1] for the last we have nums[-1]*nums[i]*nums[n].
//OK. Think about n balloons if i is the last one to burst, what now?
//We can see that the balloons is again separated into 2 sections. But this time since the balloon i is the last balloon of all to burst, the left and right //section now has well defined boundary and do not affect each other! Therefore we can do either recursive method with memoization or dp.
class Solution {
public int maxCoins(int[] nums) {
int[] nums2 = new int[nums.length+2];
int n = 1;
//get rid of all the element of 0.
for(int num: nums){
if(num>0) nums2[n++]=num;
}
//set head and tail as 1;
nums2[0]= nums2[n++] = 1;
//dp[i][j] means max coins can get from all balloons from i to j(excluded).
int[][] dp = new int[n][n];
//gap starting from 2
for(int k = 2;k<n;k++){
//start from head to iterate through tail.
for(int left = 0;left<n-k;left++){
int right = left + k;
//search all possible position that burst last.
for(int i = left+1;i<right;i++){
//find the max
dp[left][right] = Math.max(
dp[left][right],
//burst all in left and right, then last step is to burst the ith balloon.
nums2[left] * nums2[i] * nums2[right] + dp[left][i] + dp[i][right]
);
}
}
}
return dp[0][n-1];
}
}
2020-03-09
338. Counting Bits
Description
Given a non negative integer number num. For every numbers i in the range 0 ≤ i ≤ num calculate the number of 1’s in their binary representation and return them as an array.
Example 1:
Input: 2
Output: [0,1,1]
Example 2:
Input: 5
Output: [0,1,1,2,1,2]
Follow up:
It is very easy to come up with a solution with run time O(n*sizeof(integer)). But can you do it in linear time O(n) /possibly in a single pass?
Space complexity should be O(n).
Can you do it like a boss? Do it without using any builtin function like __builtin_popcount in c++ or in any other language.
Solution
//main idea is the recursion: dp[i] = dp[i/2] + i%2
class Solution {
public int[] countBits(int num) {
int[] res = new int[num+1];
for(int i =1;i<=num;i++){
res[i] = res[i/2] + i%2;
}
return res;
}
}
152. Maximum Product Subarray
Description
Given an integer array nums, find the contiguous subarray within an array (containing at least one number) which has the largest product.
Example 1:
Input: [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.
Example 2:
Input: [-2,0,-1]
Output: 0
Explanation: The result cannot be 2, because [-2,-1] is not a subarray.
Solution
class Solution {
public int maxProduct(int[] nums) {
if(nums==null || nums.length == 0) return 0;
int res = nums[0];
int a_min = nums[0], a_max = nums[0];
for(int i = 1;i<nums.length;i++){
int preMax= a_max;
//find the max possible value, start new / multiply pre_value(positive or negative)
a_max = Math.max(nums[i], Math.max(a_max * nums[i], a_min * nums[i]));
a_min = Math.min(nums[i], Math.min(preMax * nums[i], a_min * nums[i]));
res = Math.max(res, a_max);
}
return res;
}
}
279. Perfect Squares
Description
Given a positive integer n, find the least number of perfect square numbers (for example, 1, 4, 9, 16, …) which sum to n.
Example 1:
Input: n = 12
Output: 3
Explanation: 12 = 4 + 4 + 4.
Example 2:
Input: n = 13
Output: 2
Explanation: 13 = 4 + 9.
Solution
class Solution {
public int numSquares(int n) {
int[] dp = new int[n+1];
for(int i = 1;i<=n;i++){
int min = Integer.MAX_VALUE;
for(int j = 1;j*j<=i;j++){
min = Math.min(min, dp[i-j*j]+1);
}
dp[i] = min;
}
return dp[n];
}
}
120. Triangle
Description
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
Note:
Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.
Solution
class Solution {
public int minimumTotal(List<List<Integer>> triangle) {
if(triangle==null || triangle.size()==0){
return 0;
}
if(triangle.size()==1){
return triangle.get(0).get(0);
}
int[] A = new int[triangle.get(triangle.size()-1).size()+1];
//A[] is acting like a pre.
for(int i = triangle.size()-1;i>=0;i--){
List<Integer> cur = triangle.get(i);
for(int j = 0;j<cur.size();j++){
//A[j] and A[j+1] has not been updated, store previous list.
A[j] = cur.get(j) + Math.min(A[j],A[j+1]);
}
}
return A[0];
}
}
2020-03-10
95. Unique Binary Search Trees II
Description
Given an integer n, generate all structurally unique BST’s (binary search trees) that store values 1 … n.
Example:
Input: 3
Output:
[
[1,null,3,2],
[3,2,null,1],
[3,1,null,null,2],
[2,1,3],
[1,null,2,null,3]
]
Explanation:
The above output corresponds to the 5 unique BST's shown below:
1 3 3 2 1
\ / / / \ \
3 2 1 1 3 2
/ / \ \
2 1 2 3
Solution
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public List<TreeNode> generateTrees(int n) {
if(n==0) return new ArrayList();
return build(1,n);
}
public List<TreeNode> build(int start, int end){
List<TreeNode> res = new ArrayList();
if(start>end){
res.add(null);
return res;
}
//for example, build (1,2)3(4,5)
for(int idx = start;idx<=end;idx++){
//build all possible tree for node 1,2
List<TreeNode> left = build(start,idx-1);
//build all possible tree for node 4,5
List<TreeNode> right = build(idx+1,end);
for(TreeNode leftNode : left){
for(TreeNode rightNode : right){
//use 3 to build root
TreeNode cur = new TreeNode(idx);
//append all
cur.left = leftNode;
cur.right = rightNode;
res.add(cur);
}
}
}
return res;
}
}
//another idea is to use dp together with offset.
public static List<TreeNode> generateTrees(int n) {
List<TreeNode>[] result = new List[n + 1];
result[0] = new ArrayList<TreeNode>();
if (n == 0) {
return result[0];
}
result[0].add(null);
for (int len = 1; len <= n; len++) {
result[len] = new ArrayList<TreeNode>();
for (int j = 1; j <= len; j++) {
for (TreeNode nodeL : result[j-1]) {
for (TreeNode nodeR : result[len - j]) {
TreeNode node = new TreeNode(j);
node.left = nodeL;
node.right = clone(nodeR, j);
result[len].add(node);
}
}
}
}
return result[n];
}
//use offset to copy a list of subtree from offset->len.
private static TreeNode clone(TreeNode n, int offset) {
if (n == null) {
return null;
}
TreeNode node = new TreeNode(n.val + offset);
node.left = clone(n.left, offset);
node.right = clone(n.right, offset);
return node;
}
2020-03-11
307. Range Sum Query - Mutable
Description
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.
The update(i, val) function modifies nums by updating the element at index i to val.
Example:
Given nums = [1, 3, 5]
sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8
Note:
The array is only modifiable by the update function.
You may assume the number of calls to update and sumRange function is distributed evenly.
Accepted
Solution
//time complexity: O(4*logn) as there are log(n) layers and each layers will have to search 4 nodes.
class NumArray {
class TreeNode{
int start, end;
TreeNode left, right;
int sum;
TreeNode(int start, int end){
this.start = start;
this.end = end;
this.left = null;
this.right = null;
this.sum = 0;
}
}
public TreeNode buildTree(int[] nums, int start, int end){
if(start>end){
return null;
}
TreeNode cur = new TreeNode(start, end);
if(start == end){
cur.sum = nums[start];
}else{
int mid = start + (end-start)/2;
cur.left = buildTree(nums,start, mid);
cur.right = buildTree(nums,mid+1, end);
cur.sum = cur.left.sum + cur.right.sum;
}
return cur;
}
TreeNode root;
public NumArray(int[] nums) {
root = buildTree(nums,0,nums.length-1);
}
public void update(int i, int val) {
updateTree(root, i ,val);
}
public void updateTree(TreeNode root, int pos, int val){
if(root.start == root.end){
root.sum = val;
}else{
int mid = root.start + (root.end - root.start) / 2;
if(pos <= mid){
updateTree(root.left,pos,val);
}else{
updateTree(root.right, pos, val);
}
root.sum = root.left.sum + root.right.sum;
}
}
public int sumRange(int i, int j) {
return sumTree(root,i,j);
}
public int sumTree(TreeNode root, int i, int j){
if(root.start == i && root.end==j){
return root.sum;
}else{
int mid = root.start + (root.end - root.start) / 2;
if(j <= mid){
return sumTree(root.left, i,j);
}else if(i > mid){
return sumTree(root.right, i ,j);
}else{
return sumTree(root.left,i,mid) + sumTree(root.right, mid+1,j);
}
}
}
}
/**
* Your NumArray object will be instantiated and called as such:
* NumArray obj = new NumArray(nums);
* obj.update(i,val);
* int param_2 = obj.sumRange(i,j);
*/
647. Palindromic Substrings
Description
Given a string, your task is to count how many palindromic substrings in this string.
The substrings with different start indexes or end indexes are counted as different substrings even they consist of same characters.
Example 1:
Input: "abc"
Output: 3
Explanation: Three palindromic strings: "a", "b", "c".
Example 2:
Input: "aaa"
Output: 6
Explanation: Six palindromic strings: "a", "a", "a", "aa", "aa", "aaa".
Note:
The input string length won’t exceed 1000.
Solution
class Solution {
public int countSubstrings(String s) {
int len = s.length();
boolean[][] dp = new boolean[len][len];
for(int i = 0;i<len;i++){
dp[i][i]= true;
}
int count = 0;
for(int i = 0;i<len;i++){
count++;
for(int j = i-1;j>=0;j--){
if(s.charAt(i)==s.charAt(j) && (i==j+1 || dp[j+1][i-1])){
dp[j][i] = true;
count++;
}else{
dp[j][i] = false;
}
}
}
return count;
}
}
//also O(n*2) but seems faster in OJ.
class Solution {
int len;
public int countSubstrings(String s) {
int count= 0;
len = s.length();
for(int i = 0;i<len;i++){
count += countPali(s,i,i);
count += countPali(s,i,i+1);
}
return count;
}
private int countPali(String s, int left, int right){
int count=0;
while(left >= 0 && right <len && s.charAt(left)==s.charAt(right)){
count++;
left--;
right++;
}
return count;
}
}
1025. Divisor Game
Description
Alice and Bob take turns playing a game, with Alice starting first.
Initially, there is a number N on the chalkboard. On each player’s turn, that player makes a move consisting of:
Choosing any x with 0 < x < N and N % x == 0. Replacing the number N on the chalkboard with N - x. Also, if a player cannot make a move, they lose the game.
Return True if and only if Alice wins the game, assuming both players play optimally.
Example 1:
Input: 2
Output: true
Explanation: Alice chooses 1, and Bob has no more moves.
Example 2:
Input: 3
Output: false
Explanation: Alice chooses 1, Bob chooses 1, and Alice has no more moves.
Note:
1 <= N <= 1000
Solution
class Solution {
public boolean divisorGame(int N) {
//dp[i] indicates the result of the game for the given number i and for the player who started the game.
boolean[] dp = new boolean[N+1];
dp[0] = false;
dp[1] = false;
//for N, start form 2 to N;
for(int i=2; i <= N; i++){
//try all possible x, while x will not exceed i/2. x larger than i/2 will never have N%x==0.
for(int j=1; j <= i/2; j++){
if(i % j == 0){
//should choose the solution to let his opponent to lose.
if(!dp[i-j]){
dp[i] = true;
break;
}
}
}
}
return dp[N];
}
//math solution.
public boolean divisorGame(int N) {
return n%2==0;
}
}
357. Count Numbers with Unique Digits
Description
Given a non-negative integer n, count all numbers with unique digits, x, where 0 ≤ x < 10n.
Example:
Input: 2
Output: 91
Explanation: The answer should be the total numbers in the range of 0 ≤ x < 100,
excluding 11,22,33,44,55,66,77,88,99
Solution
//2-> 10 + 9*9
//3-> 10 + 9*9 + 9*9*8
//4-> 10 + 9*9 + 9*9*8 + 9*9*8*7
//...
class Solution {
public int countNumbersWithUniqueDigits(int n) {
if(n==0) return 1;
int res = 10;
int uniqueDigits = 9;
int availableNumber = 9;
while(n-- > 1 && availableNumber > 0){
uniqueDigits = uniqueDigits * availableNumber;
res += uniqueDigits;
availableNumber--;
}
return res;
}
}
91. Decode Ways
Description
A message containing letters from A-Z is being encoded to numbers using the following mapping:
‘A’ -> 1 ‘B’ -> 2 … ‘Z’ -> 26 Given a non-empty string containing only digits, determine the total number of ways to decode it.
Example 1:
Input: "12"
Output: 2
Explanation: It could be decoded as "AB" (1 2) or "L" (12).
Example 2:
Input: "226"
Output: 3
Explanation: It could be decoded as "BZ" (2 26), "VF" (22 6), or "BBF" (2 2 6).
Solution
class Solution {
public int numDecodings(String s) {
int len = s.length();
int[] dp = new int[len+1];
dp[0] = 1;
dp[1] = s.charAt(0)=='0'?0:1;
for(int i = 1; i<len;i++){
int numFirst = s.charAt(i)-'0';
int numSec = (s.charAt(i-1)-'0')* 10 + numFirst;
if(numFirst>=1 && numFirst<=9){
dp[i+1] += dp[i];
}
if(numSec>=10 && numSec<=26){
dp[i+1] += dp[i-1];
}
}
return dp[len];
}
}
2020-03-12
413. Arithmetic Slices
Description
A sequence of number is called arithmetic if it consists of at least three elements and if the difference between any two consecutive elements is the same.
For example, these are arithmetic sequence:
1, 3, 5, 7, 9
7, 7, 7, 7
3, -1, -5, -9
The following sequence is not arithmetic.
1, 1, 2, 5, 7
A zero-indexed array A consisting of N numbers is given. A slice of that array is any pair of integers (P, Q) such that 0 <= P < Q < N.
A slice (P, Q) of array A is called arithmetic if the sequence:
A[P], A[p + 1], ..., A[Q - 1], A[Q] is arithmetic. In particular, this means that P + 1 < Q.
The function should return the number of arithmetic slices in the array A.
Example:
A = [1, 2, 3, 4]
return: 3, for 3 arithmetic slices in A: [1, 2, 3], [2, 3, 4] and [1, 2, 3, 4] itself.
Solution
class Solution {
public int numberOfArithmeticSlices(int[] A) {
if(A==null || A.length<3) return 0;
int sum = 0;
int cur = 0;
for(int i = 2;i<A.length;i++){
if(A[i-1]-A[i-2] == A[i] - A[i-1]){
//1,2,3|4 -> 1+2= 3 total slices.
cur++;
sum += cur;
}else{
//end of slices, need to start new.
cur = 0;
}
}
return sum;
}
}
322. Coin Change
Description
You are given coins of different denominations and a total amount of money amount. Write a function to compute the fewest number of coins that you need to make up that amount. If that amount of money cannot be made up by any combination of the coins, return -1.
Example 1:
Input: coins = [1, 2, 5], amount = 11
Output: 3
Explanation: 11 = 5 + 5 + 1
Example 2:
Input: coins = [2], amount = 3
Output: -1
Note:
You may assume that you have an infinite number of each kind of coin.
Solution
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount+1];
Arrays.fill(dp,Integer.MAX_VALUE);
dp[0] = 0;
for(int i = 1;i<=amount;i++){
for(int coin : coins){
if(i-coin >=0 && dp[i-coin]!=Integer.MAX_VALUE){
dp[i] = Math.min(dp[i], dp[i-coin]+1);
}
}
}
return dp[amount]==Integer.MAX_VALUE?-1:dp[amount];
}
}
518. Coin Change 2
Description
You are given coins of different denominations and a total amount of money. Write a function to compute the number of combinations that make up that amount. You may assume that you have infinite number of each kind of coin.
Example 1:
Input: amount = 5, coins = [1, 2, 5]
Output: 4
Explanation: there are four ways to make up the amount:
5=5
5=2+2+1
5=2+1+1+1
5=1+1+1+1+1
Example 2:
Input: amount = 3, coins = [2]
Output: 0
Explanation: the amount of 3 cannot be made up just with coins of 2.
Example 3:
Input: amount = 10, coins = [10]
Output: 1
Note:
You can assume that
0 <= amount <= 5000 1 <= coin <= 5000 the number of coins is less than 500 the answer is guaranteed to fit into signed 32-bit integer
Solution
class Solution {
public int change(int amount, int[] coins) {
int count = coins.length;
//dp[i][j] -> use first i coins to sum to j.
int[][] dp = new int[count+1][amount+1];
//for edge case: change(0,[]);
dp[0][0] = 1;
for(int i = 1;i<=count;i++){
//base case: use i coins to sum to 0 is 1.
dp[i][0] = 1;
for(int j = 1; j<=amount;j++){
//dp[i-1][j] -> do not use this coin, use previous i-1 coins.
//dp[i][j-coins[i-1]] -> use the coin, and the total way to do it is to sum j-coins[i-1] with i coins.
dp[i][j] = dp[i-1][j] + (j-coins[i-1]>=0?dp[i][j-coins[i-1]]:0);
}
}
return dp[count][amount];
}
}
97. Interleaving String
Description
Given s1, s2, s3, find whether s3 is formed by the interleaving of s1 and s2.
Example 1:
Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
Output: true
Example 2:
Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
Output: false
Solution
class Solution {
public boolean isInterleave(String s1, String s2, String s3) {
int len1 = s1.length(), len2 = s2.length(), len3 = s3.length();
if(len1 + len2 != len3) return false;
boolean[][] dp = new boolean[len1+1][len2+1];
for(int i = 0;i<=len1;i++){
for(int j = 0;j<=len2;j++){
if(i==0 && j==0 ){
dp[i][j] = true;
}else if(i==0){
dp[i][j] = dp[i][j-1] && s2.charAt(j-1) == s3.charAt(j-1);
}else if(j==0){
dp[i][j] = dp[i-1][j] && s1.charAt(i-1) == s3.charAt(i-1);
}else{
//how to find the ribght index?
//use edge case like tail:
//dp[len1][len2] is the last of the loop, and now we have to compare the last char in s3.
//so we need to use s3.charAt(i+j-1), and s1.charAt(len1-1) and s2.charAt(len2-1);
dp[i][j] = (dp[i][j-1] && s2.charAt(j-1) == s3.charAt(i+j-1))||
(dp[i-1][j] && s1.charAt(i-1) == s3.charAt(i+j-1));
}
}
}
return dp[len1][len2];
}
}
2020-03-13
202. Happy Number
Description
Write an algorithm to determine if a number is “happy”.
A happy number is a number defined by the following process: Starting with any positive integer, replace the number by the sum of the squares of its digits, and repeat the process until the number equals 1 (where it will stay), or it loops endlessly in a cycle which does not include 1. Those numbers for which this process ends in 1 are happy numbers.
Example:
Input: 19
Output: true
Explanation:
12 + 92 = 82
82 + 22 = 68
62 + 82 = 100
12 + 02 + 02 = 1
Solution
class Solution {
//only can have two ways: end with 1 or end up in a loop;
public boolean isHappy(int n) {
int cur = n;
HashSet<Integer> seen = new HashSet();
//to check if this is a loop, if circle back, then break and return false;
while(!seen.contains(cur)){
int temp = 0;
seen.add(cur);
for(char digit: String.valueOf(cur).toCharArray()){
temp += (digit-'0')*(digit-'0');
}
//meet the final result and return true.
if(temp == 1)return true;
cur = temp;
}
return false;
}
}
2020-03-17
557. Reverse Words in a String III
Description
Given a string, you need to reverse the order of characters in each word within a sentence while still preserving whitespace and initial word order.
Example 1:
Input: "Let's take LeetCode contest"
Output: "s'teL ekat edoCteeL tsetnoc"
Note: In the string, each word is separated by single space and there will not be any extra space in the string.
Solution
class Solution {
public String reverseWords(String s) {
char[] ca = s.toCharArray();
for (int i = 0; i < ca.length; i++) {
if (ca[i] != ' ') { // when i is a non-space
int j = i;
while (j + 1 < ca.length && ca[j + 1] != ' ') { j++; } // move j to the end of the word
reverse(ca, i, j);
i = j;
}
}
return new String(ca);
}
private void reverse(char[] ca, int i, int j) {
for (; i < j; i++, j--) {
char tmp = ca[i];
ca[i] = ca[j];
ca[j] = tmp;
}
}
}
2020-03-20
654. Maximum Binary Tree
Description
Given an integer array with no duplicates. A maximum tree building on this array is defined as follow:
The root is the maximum number in the array. The left subtree is the maximum tree constructed from left part subarray divided by the maximum number. The right subtree is the maximum tree constructed from right part subarray divided by the maximum number. Construct the maximum tree by the given array and output the root node of this tree.
Example 1:
Input: [3,2,1,6,0,5]
Output: return the tree root node representing the following tree:
6
/ \
3 5
\ /
2 0
\
1
Note: The size of the given array will be in the range [1,1000].
Main Idea
If we have built the max binary tree for nums[0] ~ nums[i - 1], how can we insert nums[i] to the binary tree?
Say the max binary tree for nums[0] ~ nums[i - 1] looks like:
A
/ \
... B
/ \
... C
/ \
... ...
Say the node for nums[i] is D.
If D.val > A.val, then because A.val is at the left of D.val, we can just move the tree rooted at A to the left child of D.
D
/
A
/ \
... B
/ \
... C
/ \
... ...
If D.val < A.val, then because D.val is at the right of A.val, D must be put into the right subtree of A.
Similarly, if D.val < B.val, then D must be put into the right subtree of B.
Say B.val > D.val > C.val, then D should be the right child of B. (because D.val is at the right of B.val, and D.val is the biggest among the numbers at the right of B.val.)
Because C.val < D.val, and C.val is at the left of D.val, C should become left child of D.
A
/ \
... B
/ \
... D
/
C
/ \
... ...
So to update the max binary tree for nums[0] ~ nums[i - 1], we need to know the nodes on the right path of the tree. (A, B, C, …)
How to maintain the path?
Let’s look at the property of the nodes.
A is the biggest among nums[0] ~ nums[i - 1].
B is the biggest for the numbers between A and nums[i] (exclusive).
C is the biggest for the numbers between B and nums[i] (exclusive).
Let’s use a stack, and assume that the content of the stack contains the “right path” of nodes before the node for the current number.
For the node of the new number, we should remove the nodes in the stack which are smaller than the current number.
So we pop the stack until the top element of the stack is greater than the current number.
Then, add the node for the current number to the stack.
Solution
class Solution {
public TreeNode constructMaximumBinaryTree(int[] nums) {
Deque<TreeNode> st = new LinkedList();
for(int i = 0;i<nums.length;i++){
TreeNode cur = new TreeNode(nums[i]);
while(!st.isEmpty() && st.peek().val < nums[i]){
cur.left = st.pop();
}
if(!st.isEmpty()){
st.peek().right = cur;
}
st.push(cur);
}
return st.isEmpty() ? null : st.removeLast();
}
}
2020-03-22
463. Island Perimeter
Description
You are given a map in form of a two-dimensional integer grid where 1 represents land and 0 represents water.
Grid cells are connected horizontally/vertically (not diagonally). The grid is completely surrounded by water, and there is exactly one island (i.e., one or more connected land cells).
The island doesn’t have “lakes” (water inside that isn’t connected to the water around the island). One cell is a square with side length 1. The grid is rectangular, width and height don’t exceed 100. Determine the perimeter of the island.
Example:
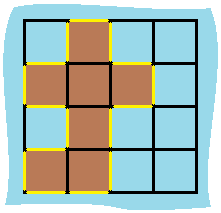
Input:
[[0,1,0,0],
[1,1,1,0],
[0,1,0,0],
[1,1,0,0]]
Output: 16
Explanation: The perimeter is the 16 yellow stripes in the image below:
Solution
class Solution {
public int islandPerimeter(int[][] grid) {
int rLen = grid.length, cLen = grid[0].length;
int count = 0;
int[][] dirs = [[0,1],[1,0],[-1,0],[0,-1]];
for(int r=0;r<rLen;r++){
for(int c=0;c<cLen;c++){
if(grid[r][c]==1){
for(int[] dir : dirs){
int new_r = r + dir[0];
int new_c = c + dir[1];
if(new_r<0 || new_r >= rLen || new_c<0 || new_c >= cLen||grid[new_r][new_c] == 0){
count++;
}
}
}
}
}
return count;
}
}
2020-03-26
394. Decode String
Description
Given an encoded string, return its decoded string.
The encoding rule is: k[encoded_string], where the encoded_string inside the square brackets is being repeated exactly k times. Note that k is guaranteed to be a positive integer.
You may assume that the input string is always valid; No extra white spaces, square brackets are well-formed, etc.
Furthermore, you may assume that the original data does not contain any digits and that digits are only for those repeat numbers, k. For example, there won’t be input like 3a or 2[4].
Examples:
s = "3[a]2[bc]", return "aaabcbc".
s = "3[a2[c]]", return "accaccacc".
s = "2[abc]3[cd]ef", return "abcabccdcdcdef".
Solution
class Solution {
public String decodeString(String s) {
String res = "";
Stack<String> stack = new Stack();
Stack<Integer> num = new Stack();
int idx = 0;
while(idx < s.length()){
char c = s.charAt(idx);
//find the repeat number
if(Character.isDigit(c)){
int count = s.charAt(idx) - '0';
idx++;
while(Character.isDigit(s.charAt(idx))){
count *= 10;
count += s.charAt(idx) - '0';
idx++;
}
num.push(count);
}else if(c=='['){
//store the previous string, and start a new one.
stack.push(res);
res = "";
idx++;
}else if(c==']'){
//finish the current one, repeat n times and append to the previous one.
StringBuilder sb = new StringBuilder(stack.pop());
int repeat = num.pop();
while(repeat-->0){
sb.append(res);
}
res = sb.toString();
idx++;
}else{
//simply a char, append to res.
res += c;
idx++;
}
}
return res;
}
}
959. Regions Cut By Slashes
Description
In a N x N grid composed of 1 x 1 squares, each 1 x 1 square consists of a /, \, or blank space. These characters divide the square into contiguous regions.
(Note that backslash characters are escaped, so a \ is represented as “\”.)
Return the number of regions.
Example 1:
Input: [ “ /”, “/ “ ] Output: 2 Explanation: The 2x2 grid is as follows:

Example 2:
Input:
[
“ /”,
“ “
]
Output: 1
Explanation: The 2x2 grid is as follows:
 Example 3:
Example 3:
Input:
[
“\/”,
“/\”
]
Output: 4
Explanation: (Recall that because \ characters are escaped, “\/” refers to \/, and “/\” refers to /.)
The 2x2 grid is as follows:

Example 4:
Input:
[
“/\”,
“\/”
]
Output: 5
Explanation: (Recall that because \ characters are escaped, “/\” refers to /\, and “\/” refers to \/.)
The 2x2 grid is as follows:

Example 5:
Input:
[
“//”,
“/ “
]
Output: 3
Explanation: The 2x2 grid is as follows:

Note:
1 <= grid.length == grid[0].length <= 30 grid[i][j] is either ‘/’, ‘', or ‘ ‘.
Solution
class Solution {
public int regionsBySlashes(String[] grid) {
int len = grid.length;
int[][] grid_new = new int[len*3][len*3];
for(int i = 0;i<len;i++){
String str = grid[i];
for(int j = 0;j<str.length();j++){
char c = str.charAt(j);
if(c == '\\'){
grid_new[j*3][i*3] = 1;
grid_new[j*3+1][i*3+1] = 1;
grid_new[j*3+2][i*3+2] = 1;
}else if(c == '/'){
grid_new[j*3][i*3+2] = 1;
grid_new[j*3+1][i*3+1] = 1;
grid_new[j*3+2][i*3] = 1;
}
}
}
int count = 0;
for(int i = 0;i<grid_new.length;i++){
for(int j = 0;j<grid_new[i].length;j++){
if(grid_new[i][j] == 0){
count++;
destroyIsland(grid_new,i,j);
}
}
}
return count;
}
private void destroyIsland(int[][] grid,int i, int j){
if(i<0 || j < 0 || i >= grid.length || j>=grid[i].length ||grid[i][j]!=0){
return;
}
grid[i][j] = 1;
destroyIsland(grid,i-1,j);
destroyIsland(grid,i+1,j);
destroyIsland(grid,i,j-1);
destroyIsland(grid,i,j+1);
}
}
2020-03-27
114. Flatten Binary Tree to Linked List
Description
Given a binary tree, flatten it to a linked list in-place.
For example, given the following tree:
1
/ \
2 5
/ \ \
3 4 6
The flattened tree should look like:
1
\
2
\
3
\
4
\
5
\
6
Solution
class Solution {
public static void flatten(TreeNode root) {
if (root == null) {return;}
flatten(root.left);
flatten(root.right);
TreeNode right = root.right;
if (root.left != null) {
root.right = root.left;
TreeNode tail = root;
while (tail.right != null) {
tail = tail.right;
}
tail.right = right;
root.left = null;
}
}
TreeNode pre;
public static void flatten(TreeNode root) {
if (root == null) {
return;
}
flatten(root.right);
flatten(root.left);
root.right = pre;
root.left = null;
pre = root;
}
}
1
/ \
2 5
/ \ \
3 4 6
-----------
pre = 5
cur = 4
1
/
2
/ \
3 4
\
5
\
6
-----------
pre = 4
cur = 3
1
/
2
/
3
\
4
\
5
\
6
-----------
cur = 2
pre = 3
1
/
2
\
3
\
4
\
5
\
6
-----------
cur = 1
pre = 2
1
\
2
\
3
\
4
\
5
\
6
2020-03-28
547. Friend Circles
Description
There are N students in a class. Some of them are friends, while some are not. Their friendship is transitive in nature. For example, if A is a direct friend of B, and B is a direct friend of C, then A is an indirect friend of C. And we defined a friend circle is a group of students who are direct or indirect friends.
Given a N*N matrix M representing the friend relationship between students in the class. If M[i][j] = 1, then the ith and jth students are direct friends with each other, otherwise not. And you have to output the total number of friend circles among all the students.
Example 1: Input: [[1,1,0], [1,1,0], [0,0,1]] Output: 2 Explanation:The 0th and 1st students are direct friends, so they are in a friend circle. The 2nd student himself is in a friend circle. So return 2. Example 2: Input: [[1,1,0], [1,1,1], [0,1,1]] Output: 1 Explanation:The 0th and 1st students are direct friends, the 1st and 2nd students are direct friends, so the 0th and 2nd students are indirect friends. All of them are in the same friend circle, so return 1. Note: N is in range [1,200]. M[i][i] = 1 for all students. If M[i][j] = 1, then M[j][i] = 1.
Solution
class Solution {
public int findCircleNum(int[][] M) {
int[] visited = new int[M.length];
int count = 0;
for (int i = 0; i < M.length; i++) {
if (visited[i] == 0) {
dfs(M, visited, i);
count++;
}
}
return count;
}
public void dfs(int[][] M, int[] visited, int i) {
for (int j = 0; j < M.length; j++) {
if (M[i][j] == 1 && visited[j] == 0) {
visited[j] = 1;
dfs(M, visited, j);
}
}
}
//another approach using union to find the common ancester.
//slower.
public int findCircleNum(int[][] M) {
int[] parents = new int[M.length];
Arrays.fill(parents, -1);
for (int i = 0; i < M.length; i++) {
for (int j = i+1; j < M.length; j++) {
if (M[i][j] == 1 && i != j) {
union(parents, i, j);
}
}
}
int count = 0;
for (int i = 0; i < parents.length; i++) {
if (parents[i] == -1)
count++;
}
return count;
}
public int find(int[] parents, int i){
if(parents[i] == -1){
return i;
}
return find(parents,parents[i]);
}
public void union(int[] parents, int x, int y){
int xset = find(parents, x);
int yset = find(parents, y);
if(xset != yset){
parents[xset] = yset;
}
}
}
116. Populating Next Right Pointers in Each Node
Description
You are given a perfect binary tree where all leaves are on the same level, and every parent has two children. The binary tree has the following definition:
struct Node { int val; Node *left; Node *right; Node *next; } Populate each next pointer to point to its next right node. If there is no next right node, the next pointer should be set to NULL.
Initially, all next pointers are set to NULL.
Follow up:
You may only use constant extra space. Recursive approach is fine, you may assume implicit stack space does not count as extra space for this problem.
Example 1:
Input: root = [1,2,3,4,5,6,7] Output: [1,#,2,3,#,4,5,6,7,#] Explanation: Given the above perfect binary tree (Figure A), your function should populate each next pointer to point to its next right node, just like in Figure B. The serialized output is in level order as connected by the next pointers, with ‘#’ signifying the end of each level.
Constraints:
The number of nodes in the given tree is less than 4096. -1000 <= node.val <= 1000
Solution
class Solution {
public Node connect(Node root) {
Node level = root;
while(level != null){
Node cur = level;
while(cur != null){
if(cur.left != null){
cur.left.next = cur.right;
}
if(cur.right != null && cur.next!=null){
cur.right.next = cur.next.left;
}
cur = cur.next;
}
level = level.left;
}
return root;
}
}
968. Binary Tree Cameras
Description
Given a binary tree, we install cameras on the nodes of the tree.
Each camera at a node can monitor its parent, itself, and its immediate children.
Calculate the minimum number of cameras needed to monitor all nodes of the tree.
Example 1:
Input: [0,0,null,0,0] Output: 1

Explanation: One camera is enough to monitor all nodes if placed as shown. Example 2:
Input: [0,0,null,0,null,0,null,null,0] Output: 2

Explanation: At least two cameras are needed to monitor all nodes of the tree. The above image shows one of the valid configurations of camera placement.
Note:
The number of nodes in the given tree will be in the range [1, 1000]. Every node has value 0.
Solution
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
//dfs is a function to return the status of the intake root;
//0 -> leaf/ node not covered.
//1 -> middle layer, parent of a leaf, with a camera on it.
//2 -> parent of a camera, covered without a camera.
class Solution {
int res;
public int minCameraCover(TreeNode root) {
res = 0;
//if root is 0 means root not covered, add extra one.
//res need to go behind dfs since dfs will change res.
return (dfs(root)==0?1:0) + res;
}
public int dfs(TreeNode root){
if(root==null) return 2;
int left = dfs(root.left);
int right = dfs(root.right);
if(left == 0 || right == 0){
res++;
return 1;
}
return (left == 1 || right == 1)?2: 0;
}
}
979. Distribute Coins in Binary Tree
Description
Given the root of a binary tree with N nodes, each node in the tree has node.val coins, and there are N coins total.
In one move, we may choose two adjacent nodes and move one coin from one node to another. (The move may be from parent to child, or from child to parent.)
Return the number of moves required to make every node have exactly one coin.
Example 1:
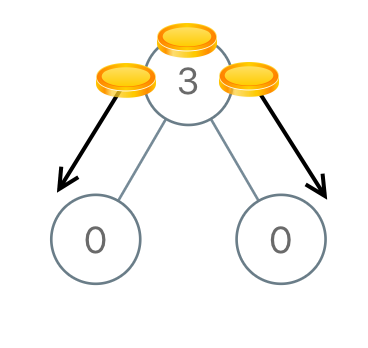
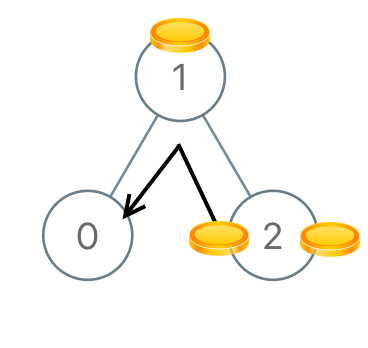
Input: [3,0,0] Output: 2 Explanation: From the root of the tree, we move one coin to its left child, and one coin to its right child. Example 2:
Input: [0,3,0] Output: 3 Explanation: From the left child of the root, we move two coins to the root [taking two moves]. Then, we move one coin from the root of the tree to the right child. Example 3:
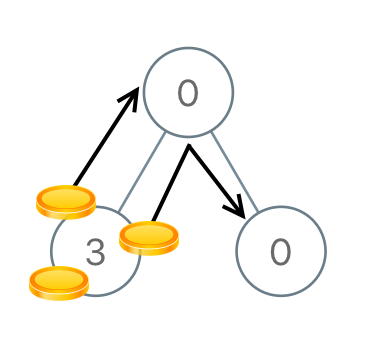
Input: [1,0,2] Output: 2 Example 4:
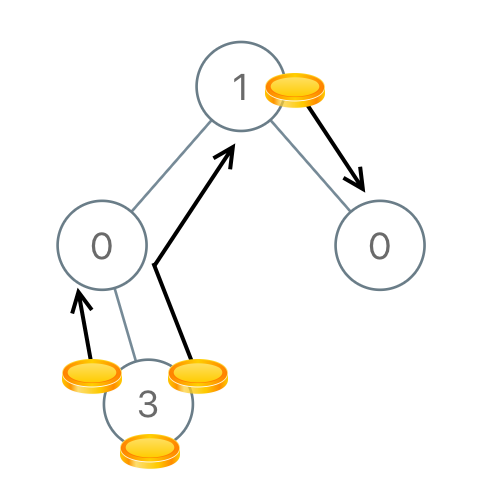
Input: [1,0,0,null,3] Output: 4
Note:
1<= N <= 100 0 <= node.val <= N
Solution
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
int res;
public int distributeCoins(TreeNode root) {
res = 0;
dfs(root);
return res;
}
//dfs will return the total difference between # of node and actual money they have.
public int dfs(TreeNode root){
if(root==null) return 0;
int left = dfs(root.left);
int right = dfs(root.right);
//how many moves to balence
res+= Math.abs(left);
res+= Math.abs(right);
//return the difference.
return left+right+root.val-1;
}
}
2020-03-29
339. Nested List Weight Sum
Description
Given a nested list of integers, return the sum of all integers in the list weighted by their depth.
Each element is either an integer, or a list – whose elements may also be integers or other lists.
Example 1:
Input: [[1,1],2,[1,1]]
Output: 10
Explanation: Four 1's at depth 2, one 2 at depth 1.
Example 2:
Input: [1,[4,[6]]]
Output: 27
Explanation: One 1 at depth 1, one 4 at depth 2, and one 6 at depth 3; 1 + 4*2 + 6*3 = 27.
Solution
/**
* // This is the interface that allows for creating nested lists.
* // You should not implement it, or speculate about its implementation
* public interface NestedInteger {
* // Constructor initializes an empty nested list.
* public NestedInteger();
*
* // Constructor initializes a single integer.
* public NestedInteger(int value);
*
* // @return true if this NestedInteger holds a single integer, rather than a nested list.
* public boolean isInteger();
*
* // @return the single integer that this NestedInteger holds, if it holds a single integer
* // Return null if this NestedInteger holds a nested list
* public Integer getInteger();
*
* // Set this NestedInteger to hold a single integer.
* public void setInteger(int value);
*
* // Set this NestedInteger to hold a nested list and adds a nested integer to it.
* public void add(NestedInteger ni);
*
* // @return the nested list that this NestedInteger holds, if it holds a nested list
* // Return null if this NestedInteger holds a single integer
* public List<NestedInteger> getList();
* }
*/
class Solution {
public int depthSum(List<NestedInteger> nestedList) {
int res = 0;
for(NestedInteger cur: nestedList){
res += dfs(cur, 1);
}
return res;
}
public int dfs(NestedInteger root, int level){
if(root.isInteger()) return root.getInteger() * level;
int res = 0;
for(NestedInteger cur: root.getList()){
res += dfs(cur, level+1);
}
return res;
}
}
2020-03-30
257. Binary Tree Paths
Description
Given a binary tree, return all root-to-leaf paths.
Note: A leaf is a node with no children.
Example:
Input:
1
/ \
2 3
\
5
Output: ["1->2->5", "1->3"]
Explanation: All root-to-leaf paths are: 1->2->5, 1->3
Solution
class Solution {
final String split = "->";
public List<String> binaryTreePaths(TreeNode root){
List<String> res = new ArrayList();
if(root == null) return res;
if(root.left == null && root.right == null){
res.add(String.valueOf(root.val));
return res;
}
if(root.left != null){
List<String> leftPath = binaryTreePaths(root.left);
for(String s:leftPath){
res.add(root.val+split+s);
}
}
if(root.right != null){
List<String> rightPath = binaryTreePaths(root.right);
for(String s:rightPath){
res.add(root.val+split+s);
}
}
return res;
}
}
class Solution {
public List<String> binaryTreePaths(TreeNode root) {
List<String> answer = new ArrayList<String>();
if (root != null) searchBT(root, "", answer);
return answer;
}
private void searchBT(TreeNode root, String path, List<String> answer) {
if (root.left == null && root.right == null) answer.add(path + root.val);
if (root.left != null) searchBT(root.left, path + root.val + "->", answer);
if (root.right != null) searchBT(root.right, path + root.val + "->", answer);
}
}
679. 24 Game
Description
You have 4 cards each containing a number from 1 to 9. You need to judge whether they could operated through *, \/, +, -, (, ) to get the value of 24.
Example 1:
Input: [4, 1, 8, 7]
Output: True
Explanation: (8-4) * (7-1) = 24
Example 2:
Input: [1, 2, 1, 2]
Output: False
Note:
The division operator / represents real division, not integer division. For example, 4 / (1 - 2/3) = 12.
Every operation done is between two numbers. In particular, we cannot use - as a unary operator. For example, with [1, 1, 1, 1] as input, the expression -1 - 1 - 1 - 1 is not allowed.
You cannot concatenate numbers together. For example, if the input is [1, 2, 1, 2], we cannot write this as 12 + 12.
