- 2020-06-01
- 2020-06-03
- 2020-06-04
- 2020-06-05
- 2020-06-07
- 2020-06-09
- 2020-06-10
- 2020-06-11
- 2020-06-12
- 2020-06-13
- 2020-06-14
- 2020-06-15
2020-06-01
346. Moving Average from Data Stream
Description
Given a stream of integers and a window size, calculate the moving average of all integers in the sliding window.
Example:
MovingAverage m = new MovingAverage(3);
m.next(1) = 1
m.next(10) = (1 + 10) / 2
m.next(3) = (1 + 10 + 3) / 3
m.next(5) = (10 + 3 + 5) / 3
Solution
class MovingAverage {
int size;
int count;
int runningSum;
Deque<Integer> deque;
/**
* Initialize your data structure here.
*/
public MovingAverage(int size) {
this.size = size;
count = 0;
runningSum = 0;
deque = new ArrayDeque<>(size);
}
public double next(int val) {
if (count < size) {
count++;
runningSum += val;
deque.addLast(val);
} else {
int prev = deque.pollFirst();
runningSum -= prev;
runningSum += val;
deque.addLast(val);
}
return (double)runningSum / (double)count;
}
}
/**
* Your MovingAverage object will be instantiated and called as such: MovingAverage obj = new MovingAverage(size); double param_1 = obj.next(val);
*/public class MovingAverage {
private int [] window;
private int n, insert;
private long sum;
/** Initialize your data structure here. */
public MovingAverage(int size) {
window = new int[size];
insert = 0;
sum = 0;
}
public double next(int val) {
if (n < window.length) n++;
sum -= window[insert];
sum += val;
window[insert] = val;
insert = (insert + 1) % window.length;
return (double)sum / n;
}
}
706. Design HashMap
Description
Design a HashMap without using any built-in hash table libraries.
To be specific, your design should include these functions:
put(key, value) : Insert a (key, value) pair into the HashMap. If the value already exists in the HashMap, update the value.
get(key): Returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key.
remove(key) : Remove the mapping for the value key if this map contains the mapping for the key.
Example:
MyHashMap hashMap = new MyHashMap();
hashMap.put(1, 1);
hashMap.put(2, 2);
hashMap.get(1); // returns 1
hashMap.get(3); // returns -1 (not found)
hashMap.put(2, 1); // update the existing value
hashMap.get(2); // returns 1
hashMap.remove(2); // remove the mapping for 2
hashMap.get(2); // returns -1 (not found)
Note:
All keys and values will be in the range of [0, 1000000].
The number of operations will be in the range of [1, 10000].
Please do not use the built-in HashMap library.
Solution
class MyHashMap {
Node[] map;
int size = 1 << 10;
/**
* Initialize your data structure here.
*/
public MyHashMap() {
map = new Node[size];
}
/**
* value will always be non-negative.
*/
public void put(int key, int value) {
int idx = indexOf(key);
if (map[idx] == null) {
map[idx] = new Node(key, value);
} else {
Node temp = map[idx];
Node pre = null;
while (temp != null) {
if(temp.key==key){
temp.val = value;
return;
}
pre = temp;
temp = temp.next;
}
pre.next = new Node(key, value);
}
}
/**
* Returns the value to which the specified key is mapped, or -1 if this map contains no mapping for the key
*/
public int get(int key) {
int idx = indexOf(key);
if (map[idx] == null) {
return -1;
} else {
Node temp = map[idx];
while (temp != null) {
if (temp.key == key) {
return temp.val;
}
temp = temp.next;
}
}
return -1;
}
/**
* Removes the mapping of the specified value key if this map contains a mapping for the key
*/
public void remove(int key) {
int idx = indexOf(key);
if (map[idx] == null) {
return;
} else{
Node dummy = new Node(-1,-1);
dummy.next = map[idx];
Node pre = dummy;
Node temp = map[idx];
while(temp!=null){
if(temp.key==key){
pre.next = temp.next;
break;
}
pre = temp;
temp = temp.next;
}
map[idx] = dummy.next;
}
}
private int indexOf(int key) {
return Integer.hashCode(key) & (size - 1);
}
public class Node {
int key;
int val;
Node next;
public Node(int key, int val) {
this.key = key;
this.val = val;
next = null;
}
}
}
/**
* Your MyHashMap object will be instantiated and called as such: MyHashMap obj = new MyHashMap(); obj.put(key,value); int param_2 = obj.get(key);
* obj.remove(key);
*/
2020-06-03
251. Flatten 2D Vector
Design
Design and implement an iterator to flatten a 2d vector. It should support the following operations: next and hasNext.
Example:
Vector2D iterator = new Vector2D([[1,2],[3],[4]]);
iterator.next(); // return 1
iterator.next(); // return 2
iterator.next(); // return 3
iterator.hasNext(); // return true
iterator.hasNext(); // return true
iterator.next(); // return 4
iterator.hasNext(); // return false
Notes:
Please remember to RESET your class variables declared in Vector2D, as static/class variables are persisted across multiple test cases. Please see here for more details.
You may assume that next() call will always be valid, that is, there will be at least a next element in the 2d vector when next() is called.
Solution
class Vector2D {
int row;
int col;
int[][] data;
public Vector2D(int[][] v) {
data = v;
row = 0;
col = 0;
}
public int next() {
hasNext();
int ret = data[row][col];
//move to next, may not be valid.
//will have to ask hasNext() to find next valid position.
col++;
if(col>=data[row].length){
col = 0;
row++;
}
return ret;
}
//after calling hasNext, if return true, then col/row will always be valid and can be retrived.
public boolean hasNext() {
//reached the end.
if(row >= data.length){
return false;
}
//col reached the tail of the current list, will go for next line.
if(col>=data[row].length){
col = 0;
//to handle next is empty list.
while(row<data.length && data[row].length==0){
row++;
}
}
//after all the search and reached the end, no valid item.
if(row >= data.length){
return false;
}
return true;
}
}
/**
* Your Vector2D object will be instantiated and called as such: Vector2D obj = new Vector2D(v); int param_1 = obj.next(); boolean param_2 = obj.hasNext();
*/
170. Two Sum III - Data structure design
Design
Design and implement a TwoSum class. It should support the following operations: add and find.
add - Add the number to an internal data structure.
find - Find if there exists any pair of numbers which sum is equal to the value.
Example 1:
add(1); add(3); add(5);
find(4) -> true
find(7) -> false
Example 2:
add(3); add(1); add(2);
find(3) -> true
find(6) -> false
Solution
There has to be one operation’s time complexity is O(n) and the other is O(1), no matter add or find.
So clearly there’s trade off when solve this problem, prefer quick find or quick add.
//consider more find and less add or we only care time complexity in finding.
//
//For example, add operation can be pre-done.
public class TwoSum {
Set<Integer> sum;
Set<Integer> num;
TwoSum(){
sum = new HashSet<Integer>();
num = new HashSet<Integer>();
}
// Add the number to an internal data structure.
//O(n) since add() is less than find();
public void add(int number) {
if(num.contains(number)){
sum.add(number * 2);
}else{
Iterator<Integer> iter = num.iterator();
while(iter.hasNext()){
sum.add(iter.next() + number);
}
num.add(number);
}
}
// Find if there exists any pair of numbers which sum is equal to the value.
public boolean find(int value) {
return sum.contains(value);
}
}
//more add and less find
public class TwoSum {
Map<Integer,Integer> hm;
TwoSum(){
hm = new HashMap<Integer,Integer>();
}
// Add the number to an internal data structure.
public void add(int number) {
if(hm.containsKey(number)){
hm.put(number,2);
}else{
hm.put(number,1);
}
}
// Find if there exists any pair of numbers which sum is equal to the value.
public boolean find(int value) {
Iterator<Integer> iter = hm.keySet().iterator();
while(iter.hasNext()){
int num1 = iter.next();
int num2 = value - num1;
//handle special case where same number added twice.
if(hm.containsKey(num2)){
if(num1 != num2 || hm.get(num2) == 2){
return true;
}
}
}
return false;
}
}
379. Design Phone Directory
Design
Design a Phone Directory which supports the following operations:
get: Provide a number which is not assigned to anyone.
check: Check if a number is available or not.
release: Recycle or release a number.
Example:
// Init a phone directory containing a total of 3 numbers: 0, 1, and 2.
PhoneDirectory directory = new PhoneDirectory(3);
// It can return any available phone number. Here we assume it returns 0.
directory.get();
// Assume it returns 1.
directory.get();
// The number 2 is available, so return true.
directory.check(2);
// It returns 2, the only number that is left.
directory.get();
// The number 2 is no longer available, so return false.
directory.check(2);
// Release number 2 back to the pool.
directory.release(2);
// Number 2 is available again, return true.
directory.check(2);
Solution
import java.util.*;
class PhoneDirectory {
Set<Integer> used = new HashSet<Integer>();
Queue<Integer> available = new LinkedList<Integer>();
int max;
public PhoneDirectory(int maxNumbers) {
max = maxNumbers;
for (int i = 0; i < maxNumbers; i++) {
available.offer(i);
}
}
public int get() {
Integer ret = available.poll();
if (ret == null) {
return -1;
}
used.add(ret);
return ret;
}
public boolean check(int number) {
if (number >= max || number < 0) {
return false;
}
return !used.contains(number);
}
public void release(int number) {
if (used.remove(number)) {
available.offer(number);
}
}
}
/**
* Your PhoneDirectory object will be instantiated and called as such:
* PhoneDirectory obj = new PhoneDirectory(maxNumbers);
* int param_1 = obj.get();
* boolean param_2 = obj.check(number);
* obj.release(number);
*/
2020-06-04
1043. Partition Array for Maximum Sum
Description
Given an integer array A, you partition the array into (contiguous) subarrays of length at most K. After partitioning, each subarray has their values changed to become the maximum value of that subarray.
Return the largest sum of the given array after partitioning.
Example 1:
Input: A = [1,15,7,9,2,5,10], K = 3
Output: 84
Explanation: A becomes [15,15,15,9,10,10,10]
Note:
1 <= K <= A.length <= 500
0 <= A[i] <= 10^6
Solution
//dp[i] -> max sum can get from A[0,i]
class Solution {
public int maxSumAfterPartitioning(int[] A, int K) {
int[] dp = new int[A.length];
for (int i = 0; i < A.length; i++) {
int curMax = 0;
for (int j = 1; j <= K && i - j + 1 >= 0; j++) {
//keep track of the max backward.
curMax = Math.max(curMax, A[i - j + 1]);
//if go beyond the head, just add 0;
dp[i] = Math.max(dp[i], curMax * j + ((i>=j)?dp[i - j]:0));
}
}
return dp[A.length-1];
}
}
399. Evaluate Division
Design
Equations are given in the format A / B = k, where A and B are variables represented as strings, and k is a real number (floating point number). Given some queries, return the answers. If the answer does not exist, return -1.0.
Example:
Given a / b = 2.0, b / c = 3.0.
queries are: a / c = ?, b / a = ?, a / e = ?, a / a = ?, x / x = ? .
return [6.0, 0.5, -1.0, 1.0, -1.0 ].
The input is: vector<pair<string, string>> equations, vector<double>& values, vector<pair<string, string>> queries , where equations.size() == values.size(), and the values are positive. This represents the equations. Return vector<double>.
According to the example above:
equations = [ ["a", "b"], ["b", "c"] ],
values = [2.0, 3.0],
queries = [ ["a", "c"], ["b", "a"], ["a", "e"], ["a", "a"], ["x", "x"] ].
The input is always valid. You may assume that evaluating the queries will result in no division by zero and there is no contradiction.
Solution
class Solution {
public double[] calcEquation(List<List<String>> equations, double[] values,
List<List<String>> queries) {
Map<String, Map<String, Double>> graph = buildGraph(equations, values);
double[] result = new double[queries.size()];
for (int i = 0; i < queries.size(); i++) {
result[i] = getPathWeight(queries.get(i).get(0), queries.get(i).get(1), new HashSet<String>(), graph);
}
return result;
}
//DFS
private double getPathWeight(String start, String end, Set<String> visited, Map<String, Map<String, Double>> graph) {
//base case where node dose not exist.
if (!graph.containsKey(start)) {
return -1.0;
}
//end case where reached the end.
if (graph.get(start).containsKey(end)) {
return graph.get(start).get(end);
}
//mark as visited.
visited.add(start);
//travers the neighbors.
for (Map.Entry<String, Double> neighbor : graph.get(start).entrySet()) {
if (!visited.contains(neighbor.getKey())) {
//get value from neighbor to end
double weight = getPathWeight(neighbor.getKey(), end, visited, graph);
//if the neighbor have path to end, just multiply the value with value[cur, neighbor].
if (weight != -1.0) {
return weight * neighbor.getValue();
}
}
}
return -1.0;
}
//build weighted graph with bi-direction.
private Map<String, Map<String, Double>> buildGraph(List<List<String>> equations, double[] values) {
Map<String, Map<String, Double>> graph = new HashMap<>();
String u, v;
for (int i = 0; i < equations.size(); i++) {
u = equations.get(i).get(0);
v = equations.get(i).get(1);
graph.putIfAbsent(u, new HashMap<>());
graph.putIfAbsent(v, new HashMap<>());
graph.get(u).put(v, values[i]);
graph.get(v).put(u, 1 / values[i]);
}
return graph;
}
}
332. Reconstruct Itinerary
Design
Given a list of airline tickets represented by pairs of departure and arrival airports [from, to], reconstruct the itinerary in order. All of the tickets belong to a man who departs from JFK. Thus, the itinerary must begin with JFK.
Note:
If there are multiple valid itineraries, you should return the itinerary that has the smallest lexical order when read as a single string. For example, the itinerary ["JFK", "LGA"] has a smaller lexical order than ["JFK", "LGB"].
All airports are represented by three capital letters (IATA code).
You may assume all tickets form at least one valid itinerary.
Example 1:
Input: [["MUC", "LHR"], ["JFK", "MUC"], ["SFO", "SJC"], ["LHR", "SFO"]]
Output: ["JFK", "MUC", "LHR", "SFO", "SJC"]
Example 2:
Input: [["JFK","SFO"],["JFK","ATL"],["SFO","ATL"],["ATL","JFK"],["ATL","SFO"]]
Output: ["JFK","ATL","JFK","SFO","ATL","SFO"]
Explanation: Another possible reconstruction is ["JFK","SFO","ATL","JFK","ATL","SFO"].
But it is larger in lexical order.
Solution
class Solution {
List<String> res;
Map<String, PriorityQueue<String>> flights;
public List<String> findItinerary(List<List<String>> tickets) {
res = new ArrayList<>();
flights = new HashMap<>();
//construct the map with priorityqueue.
for(List<String> flight : tickets){
String from = flight.get(0);
String to = flight.get(1);
flights.putIfAbsent(from,new PriorityQueue<>());
flights.get(from).offer(to);
}
visit("JFK");
return res;
}
public void visit(String from){
//if there's flight from this city.
if(flights.containsKey(from)){
//keep flying until all tickets used.
while(!flights.get(from).isEmpty()){
visit(flights.get(from).poll());
}
}
//add the city to head.
res.add(0,from);
}
}
2020-06-05
310. Minimum Height Trees
Description
For an undirected graph with tree characteristics, we can choose any node as the root. The result graph is then a rooted tree. Among all possible rooted trees, those with minimum height are called minimum height trees (MHTs). Given such a graph, write a function to find all the MHTs and return a list of their root labels.
Format
The graph contains n nodes which are labeled from 0 to n - 1. You will be given the number n and a list of undirected edges (each edge is a pair of labels).
You can assume that no duplicate edges will appear in edges. Since all edges are undirected, [0, 1] is the same as [1, 0] and thus will not appear together in edges.
Example 1 :
Input: n = 4, edges = [[1, 0], [1, 2], [1, 3]]
0
|
1
/ \
2 3
Output: [1]
Example 2 :
Input: n = 6, edges = [[0, 3], [1, 3], [2, 3], [4, 3], [5, 4]]
0 1 2
\ | /
3
|
4
|
5
Output: [3, 4]
Note:
According to the definition of tree on Wikipedia: “a tree is an undirected graph in which any two vertices are connected by exactly one path. In other words, any connected graph without simple cycles is a tree.”
The height of a rooted tree is the number of edges on the longest downward path between the root and a leaf.
Solution
//use BFS, starting from all leaves, remove it layer by layer.
//until one or two nodes left.
class Solution {
public List<Integer> findMinHeightTrees(int n, int[][] edges) {
List<Integer> ret = new ArrayList<>();
if (n == 1) {
ret.add(0);
return ret;
}
List<HashSet<Integer>> adj = new ArrayList<HashSet<Integer>>();
for (int i = 0; i < n; i++) {
adj.add(new HashSet());
}
for(int[] edge:edges){
adj.get(edge[0]).add(edge[1]);
adj.get(edge[1]).add(edge[0]);
}
//noticable that leaves only have one adj.
for(int i = 0;i<n;i++){
if(adj.get(i).size() ==1){
ret.add(i);
}
}
while(n > 2){
//reduce the number of leaves.
n -= ret.size();
List<Integer> temp = new ArrayList<>();
for(int i : ret){
//remove the leaves.
int j = adj.get(i).iterator().next();
adj.get(j).remove(i);
//after removal, the cur node become new leaf.
if(adj.get(j).size()==1){
temp.add(j);
}
}
ret = temp;
}
return ret;
}
}
1042. Flower Planting With No Adjacent
Description
You have N gardens, labelled 1 to N. In each garden, you want to plant one of 4 types of flowers.
paths[i] = [x, y] describes the existence of a bidirectional path from garden x to garden y.
Also, there is no garden that has more than 3 paths coming into or leaving it.
Your task is to choose a flower type for each garden such that, for any two gardens connected by a path, they have different types of flowers.
Return any such a choice as an array answer, where answer[i] is the type of flower planted in the (i+1)-th garden. The flower types are denoted 1, 2, 3, or 4. It is guaranteed an answer exists.
Example 1:
Input: N = 3, paths = [[1,2],[2,3],[3,1]]
Output: [1,2,3]
Example 2:
Input: N = 4, paths = [[1,2],[3,4]]
Output: [1,2,1,2]
Example 3:
Input: N = 4, paths = [[1,2],[2,3],[3,4],[4,1],[1,3],[2,4]]
Output: [1,2,3,4]
Note:
1 <= N <= 10000
0 <= paths.size <= 20000
No garden has 4 or more paths coming into or leaving it.
It is guaranteed an answer exists.
Solution
//Greedy assign myself a color that has not been used by neighbor.
class Solution {
public int[] gardenNoAdj(int N, int[][] paths) {
//build graph first.
Map<Integer, Set<Integer>> G = new HashMap<>();
for (int i = 0; i < N; i++) {
G.put(i, new HashSet<>());
}
for (int[] p : paths) {
G.get(p[0] - 1).add(p[1] - 1);
G.get(p[1] - 1).add(p[0] - 1);
}
int[] res = new int[N];
for (int i = 0; i < N; i++) {
//in order to find available color.
int[] colors = new int[5];
//iterate neighbor to mark used color.
for (int j : G.get(i)) {
colors[res[j]] = 1;
}
//try all color, there's always a valid color available.
for (int c = 4; c > 0; --c) {
if (colors[c] == 0) {
res[i] = c;
}
}
}
return res;
}
}
2020-06-07
684. Redundant Connection
Description
In this problem, a tree is an undirected graph that is connected and has no cycles.
The given input is a graph that started as a tree with N nodes (with distinct values 1, 2, ..., N), with one additional edge added. The added edge has two different vertices chosen from 1 to N, and was not an edge that already existed.
The resulting graph is given as a 2D-array of edges. Each element of edges is a pair [u, v] with u < v, that represents an undirected edge connecting nodes u and v.
Return an edge that can be removed so that the resulting graph is a tree of N nodes. If there are multiple answers, return the answer that occurs last in the given 2D-array. The answer edge [u, v] should be in the same format, with u < v.
Example 1:
Input: [[1,2], [1,3], [2,3]]
Output: [2,3]
Explanation: The given undirected graph will be like this:
1
/ \
2 - 3
Example 2:
Input: [[1,2], [2,3], [3,4], [1,4], [1,5]]
Output: [1,4]
Explanation: The given undirected graph will be like this:
5 - 1 - 2
| |
4 - 3
Note:
The size of the input 2D-array will be between 3 and 1000.
Every integer represented in the 2D-array will be between 1 and N, where N is the size of the input array.
Solution
class Solution {
public int[] findRedundantConnection(int[][] edges) {
int[] parent = new int[edges.length+1];
for (int i = 0; i < parent.length; i++) {
parent[i] = i;
}
for (int[] edge : edges) {
int f = edge[0], t = edge[1];
int p_f = find(parent,f);
int p_t = find(parent,t);
if (p_f == p_t) {
return edge;
} else {
parent[p_f] = p_t;
}
}
return new int[2];
}
private int find(int[] parent, int f) {
if (f != parent[f]) {
parent[f] = find(parent, parent[f]);
}
return parent[f];
}
}
996. Number of Squareful Arrays
Description
Given an array A of non-negative integers, the array is squareful if for every pair of adjacent elements, their sum is a perfect square.
Return the number of permutations of A that are squareful. Two permutations A1 and A2 differ if and only if there is some index i such that A1[i] != A2[i].
Example 1:
Input: [1,17,8]
Output: 2
Explanation:
[1,8,17] and [17,8,1] are the valid permutations.
Example 2:
Input: [2,2,2]
Output: 1
Note:
1 <= A.length <= 12
0 <= A[i] <= 1e9
Solution
class Solution {
HashMap<Integer, Integer> countMap;
HashMap<Integer, Set<Integer>> sqrMap;
int count;
public int numSquarefulPerms(int[] A) {
countMap = new HashMap<>();
sqrMap = new HashMap<>();
//count all numbers and init the sqrMap
for (int num : A) {
sqrMap.putIfAbsent(num, new HashSet<>());
countMap.put(num, countMap.getOrDefault(num, 0) + 1);
}
//if sum of num1 and num2 are squarable, add to sqrMap.
for (int num1 : countMap.keySet()) {
for (int num2 : countMap.keySet()) {
double c = Math.sqrt(num1 + num2);
if (c == Math.floor(c)) {
sqrMap.get(num1).add(num2);
sqrMap.get(num2).add(num1);
}
}
}
//try all possibilities starting with different numbers.
for (int num : countMap.keySet()) {
dfs(num, A.length - 1);
}
return count;
}
public void dfs(int num, int left) {
//if reached the end, count as one possibility.
if(left==0){
count++;
return;
}
//remove/use the {num}.
countMap.put(num, countMap.get(num) - 1);
//for next possible solution, sum(num,next) is squarable.
for (int next : sqrMap.get(num)) {
//if still remaining
if (countMap.get(next) != 0) {
dfs(next, left - 1);
}
}
//revert the num for futher use.
countMap.put(num, countMap.get(num) + 1);
}
}
1168. Optimize Water Distribution in a Village
Description
There are n houses in a village. We want to supply water for all the houses by building wells and laying pipes.
For each house i, we can either build a well inside it directly with cost wells[i], or pipe in water from another well to it. The costs to lay pipes between houses are given by the array pipes, where each pipes[i] = [house1, house2, cost] represents the cost to connect house1 and house2 together using a pipe. Connections are bidirectional.
Find the minimum total cost to supply water to all houses.
Example 1:
Input: n = 3, wells = [1,2,2], pipes = [[1,2,1],[2,3,1]]
Output: 3
Explanation:
The image shows the costs of connecting houses using pipes.
The best strategy is to build a well in the first house with cost 1 and connect the other houses to it with cost 2 so the total cost is 3.
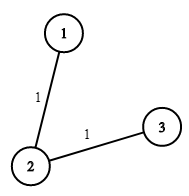
Constraints:
1 <= n <= 10000
wells.length == n
0 <= wells[i] <= 10^5
1 <= pipes.length <= 10000
1 <= pipes[i][0], pipes[i][1] <= n
0 <= pipes[i][2] <= 10^5
pipes[i][0] != pipes[i][1]
Solution
/**
take it this way:
We cannot build any well.
There is one and only one hidding well in my house (house 0).
The cost to lay pipe between house[i] and my house is wells[i].
In order to supply water to the whole village,
we need to make the village a coonected graph.
Merge all costs of pipes together and sort by key.
Greedily lay the pipes if it can connect two seperate union.
Appply union find to record which houses are connected.
*/
class Solution {
public int minCostToSupplyWater(int n, int[] wells, int[][] pipes) {
//build own edge list
List<int[]> edges = new ArrayList<>();
int[] uf = new int[n + 1];
// store pipe from HOUSE0 to house[i] with cost wells[i]
for (int i = 1; i <= n; i++) {
uf[i] = i;
edges.add(new int[]{0, i, wells[i - 1]});
}
edges.addAll(Arrays.asList(pipes));
//sorted by cost and use Greedy to pick less cost.
edges.sort((a, b) -> (a[2] - b[2]));
int res = 0;
for (int[] e : edges) {
int x = find(uf, e[0]);
int y = find(uf, e[1]);
//if(x == y means already connected, can skip.
if (x != y) {
//if not connected, add cost to res.
res += e[2];
//connect two house.
uf[x] = y;
}
}
return res;
}
private int find(int[] uf, int x) {
if (uf[x] != x) {
//find the most recent parent and store in uf[x] will save time finding.
//like a short-cut.
uf[x] = find(uf, uf[x]);
}
return uf[x];
}
}
854. K-Similar Strings
Description
Strings A and B are K-similar (for some non-negative integer K) if we can swap the positions of two letters in A exactly K times so that the resulting string equals B.
Given two anagrams A and B, return the smallest K for which A and B are K-similar.
Example 1:
Input: A = "ab", B = "ba"
Output: 1
Example 2:
Input: A = "abc", B = "bca"
Output: 2
Example 3:
Input: A = "abac", B = "baca"
Output: 2
Example 4:
Input: A = "aabc", B = "abca"
Output: 2
Note:
1 <= A.length == B.length <= 20
A and B contain only lowercase letters from the set {'a', 'b', 'c', 'd', 'e', 'f'}
Solution
//main idea: use backtrace to find the min cost to make rest of the string valid, and swap the current one.
class Solution {
public int kSimilarity(String A, String B) {
HashMap<String, Integer> dist = new HashMap<>();
return dfs(A.toCharArray(),B,dist,0);
}
private int dfs(char[] A, String B, HashMap<String, Integer> dist, int idx) {
String sa = String.valueOf(A);
//if already equal, dist is 0.
if (sa.equals(B)) {
return 0;
}
//already computed.
if (dist.containsKey(sa)) {
return dist.get(sa);
}
int min = Integer.MAX_VALUE;
//search the first index that A[i] != B[i].
while (idx < A.length && A[idx] == B.charAt(idx)) {
idx++;
}
//try all possible solution that swap with idx
for (int j = idx + 1; j < A.length; j++) {
//if can make it valid, that is A[idx] = B[idx]
if (A[j] == B.charAt(idx)) {
//swap it to make it valid.
swap(A, idx, j);
//min dist to make A.substring(idx+1,end) valid.
int next = dfs(A, B, dist, idx + 1);
//next may be MAX due to unable to make the rest string valid.
if (next != Integer.MAX_VALUE) {
min = Math.min(min, next);
}
//don't forget to swap back.
swap(A, idx, j);
}
}
dist.put(sa, min + 1);
return min + 1;
}
private void swap(char[] list, int i, int j) {
char temp = list[i];
list[i] = list[j];
list[j] = temp;
}
}
1153. String Transforms Into Another String
Description
Given two strings str1 and str2 of the same length, determine whether you can transform str1 into str2 by doing zero or more conversions.
In one conversion you can convert all occurrences of one character in str1 to any other lowercase English character.
Return true if and only if you can transform str1 into str2.
Example 1:
Input: str1 = "aabcc", str2 = "ccdee"
Output: true
Explanation: Convert 'c' to 'e' then 'b' to 'd' then 'a' to 'c'. Note that the order of conversions matter.
Example 2:
Input: str1 = "leetcode", str2 = "codeleet"
Output: false
Explanation: There is no way to transform str1 to str2.
Note:
1 <= str1.length == str2.length <= 10^4
Both str1 and str2 contain only lowercase English letters.
Solution
/**
main idea is to use map to store all the relationships between chars.
e.g. a->c, b->d, and if we encounter some relationship that is conflict to the previous existing one
like a -> b , then return false.
1. transformation of link link ,like a -> b -> c:
we do the transformation from end to begin, that is b->c then a->b
2. transformation of cycle, like a -> b -> c -> a:
in this case we need a tmp
c->tmp, b->c a->b and tmp->a
Same as the process of swap two variable.
In both case, there should at least one character that is unused,
to use it as the tmp for transformation.
So we need to return if the size of set of unused characters < 26.
*/
class Solution {
public boolean canConvert(String str1, String str2) {
if (str1.equals(str2)) {
return true;
}
Map<Character, Character> map = new HashMap<>();
int len = str1.length();
for (int i = 0; i < len; i++) {
if (!map.containsKey(str1.charAt(i))) {
map.put(str1.charAt(i), str2.charAt(i));
} else {
if (map.get(str1.charAt(i)) != str2.charAt(i)) {
return false;
}
}
}
//should exist at least one char that's unused as temp.
return new HashSet<Character>(map.values()).size() < 26;
}
}
2020-06-09
143. Reorder List
Description
Given a singly linked list L: L0→L1→…→Ln-1→Ln, reorder it to: L0→Ln→L1→Ln-1→L2→Ln-2→…
You may not modify the values in the list’s nodes, only nodes itself may be changed.
Example 1:
Given 1->2->3->4, reorder it to 1->4->2->3.
Example 2:
Given 1->2->3->4->5, reorder it to 1->5->2->4->3.
Solution
class Solution {
public void reorderList(ListNode head) {
if(head==null||head.next==null) return;
//Find the middle of the list
ListNode p1=head;
ListNode p2=head;
while(p2.next!=null&&p2.next.next!=null){
p1=p1.next;
p2=p2.next.next;
}
//Reverse the half after middle 1->2->3->4->5->6 to 1->2->3->6->5->4
ListNode preMiddle=p1;
ListNode preCurrent=p1.next;
while(preCurrent.next!=null){
ListNode current=preCurrent.next;
preCurrent.next=current.next;
current.next=preMiddle.next;
preMiddle.next=current;
}
//Start reorder one by one 1->2->3->6->5->4 to 1->6->2->5->3->4
p1=head;
p2=preMiddle.next;
while(p1!=preMiddle){
preMiddle.next=p2.next;
p2.next=p1.next;
p1.next=p2;
p1=p2.next;
p2=preMiddle.next;
}
}
}
2020-06-10
160. Intersection of Two Linked Lists
Description
Write a program to find the node at which the intersection of two singly linked lists begins.
For example, the following two linked lists:
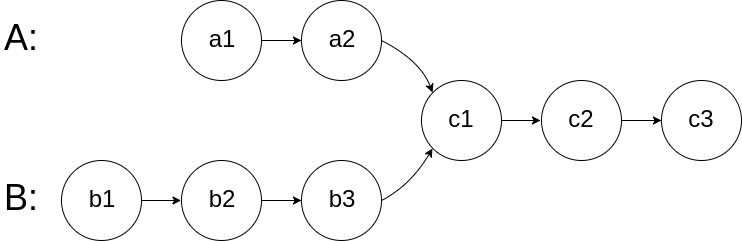
begin to intersect at node c1.
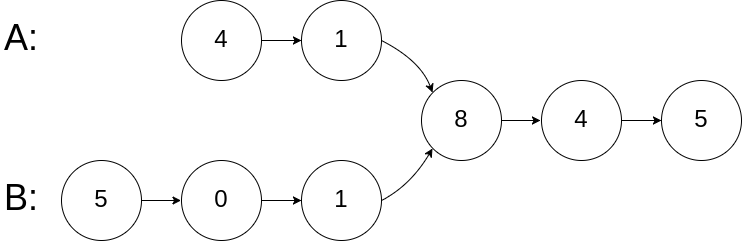
Input: intersectVal = 8, listA = [4,1,8,4,5], listB = [5,0,1,8,4,5], skipA = 2, skipB = 3
Output: Reference of the node with value = 8
Input Explanation: The intersected node's value is 8 (note that this must not be 0 if the two lists intersect). From the head of A, it reads as [4,1,8,4,5]. From the head of B, it reads as [5,0,1,8,4,5]. There are 2 nodes before the intersected node in A; There are 3 nodes before the intersected node in B.
Solution
//count the length
public class Solution {
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
int lenA = 0, lenB = 0;
ListNode curA = headA;
ListNode curB = headB;
while(curA!=null){
lenA++;
curA = curA.next;
}
while(curB!=null){
lenB++;
curB = curB.next;
}
while(lenA > lenB){
headA = headA.next;
lenA--;
}
while(lenA < lenB){
headB = headB.next;
lenB--;
}
while(headA != headB)
{
headA = headA.next;
headB = headB.next;
}
return headA;
}
}
/**
use two iterations to do that. In the first iteration
we will reset the pointer of one linkedlist to the head of another linkedlist after it reaches the tail node.
In the second iteration, we will move two pointers until they points to the same node.
Our operations in first iteration will help us counteract the difference.
So if two linkedlist intersects, the meeting point in second iteration must be the intersection point.
If the two linked lists have no intersection at all, then the meeting pointer in second iteration must be the tail node of both lists, which is null
*/
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
//boundary check
if(headA == null || headB == null) return null;
ListNode a = headA;
ListNode b = headB;
//if a & b have different len, then we will stop the loop after second iteration
while( a != b){
//for the end of first iteration, we just reset the pointer to the head of another linkedlist
a = a == null? headB : a.next;
b = b == null? headA : b.next;
}
return a;
}
218. The Skyline Problem
Description
A city’s skyline is the outer contour of the silhouette formed by all the buildings in that city when viewed from a distance. Now suppose you are given the locations and height of all the buildings as shown on a cityscape photo (Figure A), write a program to output the skyline formed by these buildings collectively (Figure B).

The geometric information of each building is represented by a triplet of integers [Li, Ri, Hi], where Li and Ri are the x coordinates of the left and right edge of the ith building, respectively, and Hi is its height. It is guaranteed that 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX, and Ri - Li > 0. You may assume all buildings are perfect rectangles grounded on an absolutely flat surface at height 0.
For instance, the dimensions of all buildings in Figure A are recorded as: [ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] .
The output is a list of "key points" (red dots in Figure B) in the format of [ [x1,y1], [x2, y2], [x3, y3], ... ] that uniquely defines a skyline. A key point is the left endpoint of a horizontal line segment. Note that the last key point, where the rightmost building ends, is merely used to mark the termination of the skyline, and always has zero height. Also, the ground in between any two adjacent buildings should be considered part of the skyline contour.
For instance, the skyline in Figure B should be represented as:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ].
Notes:
The number of buildings in any input list is guaranteed to be in the range [0, 10000].
The input list is already sorted in ascending order by the left x position Li.
The output list must be sorted by the x position.
There must be no consecutive horizontal lines of equal height in the output skyline. For instance, [...[2 3], [4 5], [7 5], [11 5], [12 7]...] is not acceptable; the three lines of height 5 should be merged into one in the final output as such: [...[2 3], [4 5], [12 7], ...]
Solution
/**
main idea is to add the height to a pile/heap when encounter the left bond
and remove when right boarder.
so inside the heap, it will have all the height for current x position.
use pq or treemap to find the max height for current position.
add to res if it's different from the previous.
*/
class Solution {
public List<List<Integer>> getSkyline(int[][] buildings) {
List<List<Integer>> res = new ArrayList<>();
List<int[]> heights = new ArrayList<>();
//add to height list, negative if right boundary.
for(int[] building : buildings){
heights.add(new int[]{building[0],building[2]});
heights.add(new int[]{building[1],-building[2]});
}
//sort based on x coord.
heights.sort((a,b)->(a[0]==b[0]?b[1]-a[1]:a[0]-b[0]));
TreeMap<Integer,Integer> map = new TreeMap<>();
//gound
map.put(0,1);
int prev = 0;
for(int[] height : heights){
if(height[1]<0){
//remove the height from heap if meet right boundary.
if(map.get(-height[1])>1){
map.put(-height[1],map.get(-height[1])-1);
}else{
map.remove(-height[1]);
}
}else{
//add to heap if left.
map.put(height[1],map.getOrDefault(height[1],0)+1);
}
//find the max height for current position.
int cur = map.lastKey();
//if it's a curcial point.
if(cur != prev){
List<Integer> temp = new ArrayList<>();
temp.add(height[0]);
temp.add(cur);
res.add(temp);
prev = cur;
}
}
return res;
}
}
313. Super Ugly Number
Description
Write a program to find the nth super ugly number.
Super ugly numbers are positive numbers whose all prime factors are in the given prime list primes of size k.
Example:
Input: n = 12, primes = [2,7,13,19]
Output: 32
Explanation: [1,2,4,7,8,13,14,16,19,26,28,32] is the sequence of the first 12
super ugly numbers given primes = [2,7,13,19] of size 4.
Note:
1 is a super ugly number for any given primes.
The given numbers in primes are in ascending order.
0 < k ≤ 100, 0 < n ≤ 106, 0 < primes[i] < 1000.
The nth super ugly number is guaranteed to fit in a 32-bit signed integer.
Solution
class Solution {
public int nthSuperUglyNumber(int n, int[] primes) {
if (n <= 0) {
return 0;
}
if (n == 1) {
return 1;
}
int[] primesIdx = new int[primes.length];
int[] dp = new int[n];
dp[0] = 1;
for (int i = 1; i < n; i++) {
int next = Integer.MAX_VALUE;
for(int idx = 0;idx<primes.length;idx++){
next = Math.min(next, dp[primesIdx[idx]] * primes[idx]);
}
for(int idx = 0;idx<primes.length;idx++){
if(next == dp[primesIdx[idx]] * primes[idx]){
primesIdx[idx]++;
}
}
dp[i] = next;
}
return dp[n-1];
}
}
857. Minimum Cost to Hire K Workers
Description
There are N workers. The i-th worker has a quality[i] and a minimum wage expectation wage[i].
Now we want to hire exactly K workers to form a paid group. When hiring a group of K workers, we must pay them according to the following rules:
Every worker in the paid group should be paid in the ratio of their quality compared to other workers in the paid group.
Every worker in the paid group must be paid at least their minimum wage expectation.
Return the least amount of money needed to form a paid group satisfying the above conditions.
Example 1:
Input: quality = [10,20,5], wage = [70,50,30], K = 2
Output: 105.00000
Explanation: We pay 70 to 0-th worker and 35 to 2-th worker.
Example 2:
Input: quality = [3,1,10,10,1], wage = [4,8,2,2,7], K = 3
Output: 30.66667
Explanation: We pay 4 to 0-th worker, 13.33333 to 2-th and 3-th workers seperately.
Note:
1 <= K <= N <= 10000, where N = quality.length = wage.length
1 <= quality[i] <= 10000
1 <= wage[i] <= 10000
Answers within 10^-5 of the correct answer will be considered correct.
Solution
// The key to the solution is that Kth ratio (wage / quality) can only satisfy workers with a smaller ratio.
// Otherwise, it will break the minimum expectation constraint, since every worker will be sharing the same ratio.
// However, you cannot simply pick the first Kth workers. Since if the sum of the quality is super high,
// then we would rather have a higher ratio but smaller sum of quality.
// Therefore, we are looking for the minimum sum of quality * ratio. Following is how the algorithm works:
// 1. Create an array that stores the ratio (worker[0]) and quality (worker[1]).
// We don't care about the min wage expectation anymore,
// since we are only looking at the workers with a ratio that is smaller than any current ratio,
// and will always satisfy the minimum constraint.
// 2. Sort the array and start from Kth smallest ratio.
// Otherwise, there won't be enough workers that satisfy with the current ratio (minimum constraint breaks)
// 3. Keep increase the current ratio with the next worker and find the smallest sum, since both the sum of quality and ratio impacts the result
// 4. Keep removing the largest quality, since we want the smallest sum of quality and the smallest ratio possible
class Solution {
public double mincostToHireWorkers(int[] quality, int[] wage, int K) {
double[][] workers = new double[quality.length][2];
for(int i = 0;i<workers.length;i++){
workers[i] = new double[]{(double)(wage[i])/quality[i],(double)(quality[i])};
}
Arrays.sort(workers,(a,b)->(Double.compare(a[0],b[0])));
double res = Double.MAX_VALUE, curSum = 0;
PriorityQueue<Double> pq = new PriorityQueue<Double>((a,b)->Double.compare(b,a));
for(double[] worker : workers){
curSum += worker[1];
pq.add(worker[1]);
if(pq.size()>K){
curSum -= pq.poll();
}
if(pq.size() == K){
//since the current ratio is larger than any of the item now
//it can guarantee that minimum wage are satisfied.
res = Math.min(res, curSum * worker[0]);
}
}
return res;
}
}
2020-06-11
373. Find K Pairs with Smallest Sums
Description
You are given two integer arrays nums1 and nums2 sorted in ascending order and an integer k.
Define a pair (u,v) which consists of one element from the first array and one element from the second array.
Find the k pairs (u1,v1),(u2,v2) …(uk,vk) with the smallest sums.
Example 1:
Input: nums1 = [1,7,11], nums2 = [2,4,6], k = 3
Output: [[1,2],[1,4],[1,6]]
Explanation: The first 3 pairs are returned from the sequence:
[1,2],[1,4],[1,6],[7,2],[7,4],[11,2],[7,6],[11,4],[11,6]
Example 2:
Input: nums1 = [1,1,2], nums2 = [1,2,3], k = 2
Output: [1,1],[1,1]
Explanation: The first 2 pairs are returned from the sequence:
[1,1],[1,1],[1,2],[2,1],[1,2],[2,2],[1,3],[1,3],[2,3]
Example 3:
Input: nums1 = [1,2], nums2 = [3], k = 3
Output: [1,3],[2,3]
Explanation: All possible pairs are returned from the sequence: [1,3],[2,3]
Solution
//main idea is to act like a list of list, which start with nums1[i]
//nums1[0]->nums2[0]->nums2[1]-> ...
//nums1[i]->nums2[0]->nums2[1]-> ...
//so can use priorityqueue to store tumple, nums1, nums2 and index for nums2
//and always extract the min value.
class Solution {
public List<List<Integer>> kSmallestPairs(int[] nums1, int[] nums2, int k) {
List<List<Integer>> res = new ArrayList<>();
if(nums1.length == 0 || nums2.length == 0 || k==0){
return res;
}
PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->(a[0]+a[1]-b[0]-b[1]));
for(int i = 0;i<nums1.length;i++){
pq.offer(new int[]{nums1[i],nums2[0],0});
}
while(k>0 && !pq.isEmpty()){
k--;
int[] cur = pq.poll();
List<Integer> temp = new ArrayList<>();
temp.add(cur[0]);
temp.add(cur[1]);
res.add(temp);
if(cur[2] + 1 ==nums2.length){
continue;
}
pq.offer(new int[]{cur[0], nums2[cur[2]+1], cur[2]+1});
}
return res;
}
}
2020-06-12
451. Sort Characters By Frequency
Description
Given a string, sort it in decreasing order based on the frequency of characters.
Example 1:
Input:
"tree"
Output:
"eert"
Explanation:
'e' appears twice while 'r' and 't' both appear once.
So 'e' must appear before both 'r' and 't'. Therefore "eetr" is also a valid answer.
Example 2:
Input:
"cccaaa"
Output:
"cccaaa"
Explanation:
Both 'c' and 'a' appear three times, so "aaaccc" is also a valid answer.
Note that "cacaca" is incorrect, as the same characters must be together.
Example 3:
Input:
"Aabb"
Output:
"bbAa"
Explanation:
"bbaA" is also a valid answer, but "Aabb" is incorrect.
Note that 'A' and 'a' are treated as two different characters.
Solution
//bucket sort
class Solution {
public String frequencySort(String s) {
Map<Character, Integer> count = new HashMap<>();
for (char ch : s.toCharArray()) {
count.put(ch, count.getOrDefault(ch, 0) + 1);
}
List<Character>[] buckets = new List[s.length() + 1];
for (char ch : count.keySet()) {
int freq = count.get(ch);
if (buckets[freq] == null) {
buckets[freq] = new ArrayList<Character>();
}
buckets[freq].add(ch);
}
StringBuilder sb = new StringBuilder();
for (int pos = buckets.length - 1; pos > 0; pos--) {
if(buckets[pos]!=null){
for(char c: buckets[pos]){
for(int i = 0;i<pos;i++){
sb.append(c);
}
}
}
}
return sb.toString();
}
}
659. Split Array into Consecutive Subsequences
Description
Given an array nums sorted in ascending order, return true if and only if you can split it into 1 or more subsequences such that each subsequence consists of consecutive integers and has length at least 3.
Example 1:
Input: [1,2,3,3,4,5]
Output: True
Explanation:
You can split them into two consecutive subsequences :
1, 2, 3
3, 4, 5
Example 2:
Input: [1,2,3,3,4,4,5,5]
Output: True
Explanation:
You can split them into two consecutive subsequences :
1, 2, 3, 4, 5
3, 4, 5
Example 3:
Input: [1,2,3,4,4,5]
Output: False
Solution
import java.util.*;
class Solution {
public boolean isPossible(int[] nums) {
Map<Integer, Integer> count = new HashMap<>();
Map<Integer, Integer> tail = new HashMap<>();
for (int num : nums) {
count.put(num, count.getOrDefault(num, 0) + 1);
}
for (int i = 0; i < nums.length; i++) {
int cur = nums[i];
//need to skip when this been used.
if(count.get(cur)==0)continue;
if(tail.containsKey(cur-1) && tail.get(cur-1)>0){
tail.put(cur-1,tail.get(cur-1)-1);
tail.put(cur,tail.getOrDefault(cur,0)+1);
count.put(cur,count.get(cur)-1);
}else if(count.getOrDefault(cur,0)>0 && count.getOrDefault(cur+1,0)>0 && count.getOrDefault(cur+2,0)>0){
tail.put(cur+2,tail.getOrDefault(cur+2,0)+1);
count.put(cur,count.get(cur)-1);
count.put(cur+1,count.get(cur+1)-1);
count.put(cur+2,count.get(cur+2)-1);
}else{
return false;
}
}
return true;
}
}
787. Cheapest Flights Within K Stops
Description
There are n cities connected by m flights. Each flight starts from city u and arrives at v with a price w.
Now given all the cities and flights, together with starting city src and the destination dst, your task is to find the cheapest price from src to dst with up to k stops. If there is no such route, output -1.
Example 1:
Input:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 1
Output: 200
Explanation:
The graph looks like this:
The cheapest price from city 0 to city 2 with at most 1 stop costs 200, as marked red in the picture.
Example 2:
Input:
n = 3, edges = [[0,1,100],[1,2,100],[0,2,500]]
src = 0, dst = 2, k = 0
Output: 500
Explanation:
The graph looks like this:
The cheapest price from city 0 to city 2 with at most 0 stop costs 500, as marked blue in the picture.
Constraints:
The number of nodes n will be in range [1, 100], with nodes labeled from 0 to n - 1.
The size of flights will be in range [0, n * (n - 1) / 2].
The format of each flight will be (src, dst, price).
The price of each flight will be in the range [1, 10000].
k is in the range of [0, n - 1].
There will not be any duplicated flights or self cycles.
Solution
class Solution {
public int findCheapestPrice(int n, int[][] flights, int src, int dst, int K) {
Map<Integer, HashMap<Integer, Integer>> map = new HashMap<>();
for (int[] pair : flights) {
HashMap<Integer,Integer> r = map.getOrDefault(pair[0],new HashMap<>());
r.put(pair[1],pair[2]);
map.put(pair[0],r);
}
PriorityQueue<int[]> pq = new PriorityQueue<>((a,b)->(a[1]-b[1]));
//store stops in the tuple so can asset whether reach max stops.
pq.offer(new int[]{src,0,K+1});
while(!pq.isEmpty()){
int[] cur =pq.poll();
int city = cur[0];
int price = cur[1];
int stops = cur[2];
if(city == dst) return price;
if(stops>0){
HashMap<Integer,Integer> adj = map.getOrDefault(city,new HashMap());
for(Map.Entry<Integer,Integer> e:adj.entrySet()){
pq.offer(new int[]{e.getKey(),price+e.getValue(),stops-1});
}
}
}
return -1;
}
}
2020-06-13
947. Most Stones Removed with Same Row or Column
Description
On a 2D plane, we place stones at some integer coordinate points. Each coordinate point may have at most one stone.
Now, a move consists of removing a stone that shares a column or row with another stone on the grid.
What is the largest possible number of moves we can make?
Example 1:
Input: stones = [[0,0],[0,1],[1,0],[1,2],[2,1],[2,2]]
Output: 5
Example 2:
Input: stones = [[0,0],[0,2],[1,1],[2,0],[2,2]]
Output: 3
Example 3:
Input: stones = [[0,0]]
Output: 0
Note:
1 <= stones.length <= 1000
0 <= stones[i][j] < 10000
Solution
//Union find, group all the stones together if they share the same col or row.
//total stone - number of island will be the max count can be removed.
class Solution {
HashMap<String, String> union;
int count;
public int removeStones(int[][] stones) {
union = new HashMap<>();
count = stones.length;
for (int[] stone : stones) {
String pos = stone[0] + " " + stone[1];
union.put(pos, pos);
}
for (int[] s1 : stones) {
String ss1 = s1[0] + " " + s1[1];
for (int[] s2 : stones) {
if (s1[0] == s2[0] || s1[1] == s2[1]) {
String ss2 = s2[0] + " " + s2[1];
union(ss1, ss2);
}
}
}
return stones.length - count;
}
private void union(String s1, String s2) {
String r1 = find(s1), r2 = find(s2);
if (r1.equals(r2)) {
return;
}
union.put(r1, r2);
count--;
}
private String find(String s) {
if (!union.get(s).equals(s)) {
union.put(s, find(union.get(s)));
}
return union.get(s);
}
}
721. Accounts Merge
Description
Given a list accounts, each element accounts[i] is a list of strings, where the first element accounts[i][0] is a name, and the rest of the elements are emails representing emails of the account.
Now, we would like to merge these accounts. Two accounts definitely belong to the same person if there is some email that is common to both accounts. Note that even if two accounts have the same name, they may belong to different people as people could have the same name. A person can have any number of accounts initially, but all of their accounts definitely have the same name.
After merging the accounts, return the accounts in the following format: the first element of each account is the name, and the rest of the elements are emails in sorted order. The accounts themselves can be returned in any order.
Example 1:
Input:
accounts = [["John", "johnsmith@mail.com", "john00@mail.com"], ["John", "johnnybravo@mail.com"], ["John", "johnsmith@mail.com", "john_newyork@mail.com"], ["Mary", "mary@mail.com"]]
Output: [["John", 'john00@mail.com', 'john_newyork@mail.com', 'johnsmith@mail.com'], ["John", "johnnybravo@mail.com"], ["Mary", "mary@mail.com"]]
Explanation:
The first and third John's are the same person as they have the common email "johnsmith@mail.com".
The second John and Mary are different people as none of their email addresses are used by other accounts.
We could return these lists in any order, for example the answer [['Mary', 'mary@mail.com'], ['John', 'johnnybravo@mail.com'],
['John', 'john00@mail.com', 'john_newyork@mail.com', 'johnsmith@mail.com']] would still be accepted.
Note:
The length of accounts will be in the range [1, 1000].
The length of accounts[i] will be in the range [1, 10].
The length of accounts[i][j] will be in the range [1, 30].
Solution
class Solution {
public List<List<String>> accountsMerge(List<List<String>> accounts) {
HashMap<String, String> parent = new HashMap<>();
HashMap<String, String> accountName = new HashMap<>();
HashMap<String, List<String>> unions = new HashMap<>();
//put all email into map.
for (List<String> account : accounts) {
String name = account.get(0);
for (int i = 1; i < account.size(); i++) {
parent.put(account.get(i), account.get(1));
accountName.put(account.get(i), name);
}
}
//union all emails belong to the same person.
//a<-b, a<-c, d<-b(parent to a, so d<-a), d<-f,
//d<-a<-b,c d<-f
for (List<String> account : accounts) {
String parentEmail = find(parent, account.get(1));
for (int i = 2; i < account.size(); i++) {
parent.put(find(parent, account.get(i)), parentEmail);
}
}
for (String email : parent.keySet()) {
String parentEmail = find(parent, email);
unions.putIfAbsent(parentEmail, new ArrayList<>());
unions.get(parentEmail).add(email);
}
List<List<String>> res = new ArrayList<>();
for (String parentEmail : unions.keySet()) {
List<String> temp = new ArrayList<>(unions.get(parentEmail));
temp.sort(String::compareTo);
temp.add(0, accountName.get(parentEmail));
res.add(temp);
}
return res;
}
private String find(Map<String, String> p, String s) {
return p.get(s).equals(s) ? s : find(p,p.get(s));
}
}
2020-06-14
924. Minimize Malware Spread
Description
In a network of nodes, each node i is directly connected to another node j if and only if graph[i][j] = 1.
Some nodes initial are initially infected by malware. Whenever two nodes are directly connected and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose M(initial) is the final number of nodes infected with malware in the entire network, after the spread of malware stops.
We will remove one node from the initial list. Return the node that if removed, would minimize M(initial). If multiple nodes could be removed to minimize M(initial), return such a node with the smallest index.
Note that if a node was removed from the initial list of infected nodes, it may still be infected later as a result of the malware spread.
Example 1:
Input: graph = [[1,1,0],[1,1,0],[0,0,1]], initial = [0,1]
Output: 0
Example 2:
Input: graph = [[1,0,0],[0,1,0],[0,0,1]], initial = [0,2]
Output: 0
Example 3:
Input: graph = [[1,1,1],[1,1,1],[1,1,1]], initial = [1,2]
Output: 1
Note:
1 < graph.length = graph[0].length <= 300
0 <= graph[i][j] == graph[j][i] <= 1
graph[i][i] == 1
1 <= initial.length <= graph.length
0 <= initial[i] < graph.length
Solution
/**
Union found all nodes.
Count the union size of each union set.
Count the malware number of each union set.
Return the biggest union's malware if there is one and only one malware.
If no such union that has and has only one malware,
return the malware with minimum index.
Time Complexity:
O(N^2)
**/
class Solution {
int[] parent;
public int minMalwareSpread(int[][] graph, int[] initial) {
int len = graph.length;
parent = new int[len];
for(int i = 0;i<len;i++){
parent[i] = i;
}
for (int i = 0; i < len; i++) {
for (int j = 0; j < len; j++) {
if (graph[i][j] == 1) {
union(i, j);
}
}
}
int[] unionSize = new int[len];
int[] malCount = new int[len];
for(int i = 0;i<len;i++){
unionSize[find(i)]++;
}
for(int init : initial){
malCount[find(init)]++;
}
int res = -1;
int maxSize = -1;
Arrays.sort(initial);
for(int init : initial){
int idx = find(init);
//if there's only one malware in the union
//and this union is the largest, so can minimize the infested node.
if(malCount[idx]==1 && unionSize[idx]>maxSize){
res = init;
maxSize = unionSize[idx];
}
}
if(maxSize!=-1){
return res;
}
return initial[0];
}
public int find(int x) {
if (parent[x] != x) {
parent[x] = find(parent[x]);
}
return parent[x];
}
public void union(int x, int y) {
int p_x = find(x);
int p_y = find(y);
if (p_x != p_y) {
parent[p_x] = p_y;
}
}
}
305. Number of Islands II
Description
A 2d grid map of m rows and n columns is initially filled with water. We may perform an addLand operation which turns the water at position (row, col) into a land. Given a list of positions to operate, count the number of islands after each addLand operation. An island is surrounded by water and is formed by connecting adjacent lands horizontally or vertically. You may assume all four edges of the grid are all surrounded by water.
Example:
Input: m = 3, n = 3, positions = [[0,0], [0,1], [1,2], [2,1]]
Output: [1,1,2,3]
Explanation:
Initially, the 2d grid grid is filled with water. (Assume 0 represents water and 1 represents land).
0 0 0
0 0 0
0 0 0
Operation #1: addLand(0, 0) turns the water at grid[0][0] into a land.
1 0 0
0 0 0 Number of islands = 1
0 0 0
Operation #2: addLand(0, 1) turns the water at grid[0][1] into a land.
1 1 0
0 0 0 Number of islands = 1
0 0 0
Operation #3: addLand(1, 2) turns the water at grid[1][2] into a land.
1 1 0
0 0 1 Number of islands = 2
0 0 0
Operation #4: addLand(2, 1) turns the water at grid[2][1] into a land.
1 1 0
0 0 1 Number of islands = 3
0 1 0
Follow up:
Can you do it in time complexity O(k log mn), where k is the length of the positions?
Solution
/**
Union all the island together as one island and count the total number of unions.
*/
class Solution {
public List<Integer> numIslands2(int m, int n, int[][] positions) {
List<Integer> res = new LinkedList<>();
if (m <= 0 || n <= 0) {
return res;
}
int count = 0;
int[] roots = new int[m * n]; // 1D array of roots
Arrays.fill(roots, -1); // Every position is water initially.
int[][] directions = new int[][][[-1, 0], [1, 0], [0, -1], [0, 1]];
for (int[] p : positions) {
int island = p[0] * n + p[1];
//in case of duplicated position.
if (roots[island] != -1) {
res.add(count);
continue;
}
roots[island] = island; // Set it to be the root of itself.
count++;
// Check four directions
for (int[] dir : directions) {
int x = p[0] + dir[0], y = p[1] + dir[1];
int neighbor = x * n + y;
// Skip when x or y is invalid, or neighbor is water.
if (x < 0 || x >= m || y < 0 || y >= n || roots[neighbor] == -1) {
continue;
}
int neighborRoot = find(neighbor, roots);
int islandRoot = find(island, roots);
if (islandRoot != neighborRoot) {
// Union by position, always append smaller one to the larger one
//so it can have the same root.
if (islandRoot >= neighborRoot) {
roots[neighborRoot] = islandRoot;
} else {
roots[islandRoot] = neighborRoot;
}
count--;
}
}
res.add(count);
}
return res;
}
private int find(int id, int[] roots) {
if (roots[id] == id) {
return id;
} else {
roots[id] = find(roots[id], roots); // path compression
return roots[id];
}
}
}
928. Minimize Malware Spread II
Description
(This problem is the same as Minimize Malware Spread, with the differences bolded.)
In a network of nodes, each node i is directly connected to another node j if and only if graph[i][j] = 1.
Some nodes initial are initially infected by malware. Whenever two nodes are directly connected and at least one of those two nodes is infected by malware, both nodes will be infected by malware. This spread of malware will continue until no more nodes can be infected in this manner.
Suppose M(initial) is the final number of nodes infected with malware in the entire network, after the spread of malware stops.
We will remove one node from the initial list, completely removing it and any connections from this node to any other node. Return the node that if removed, would minimize M(initial). If multiple nodes could be removed to minimize M(initial), return such a node with the smallest index.
Example 1:
Input: graph = [[1,1,0],[1,1,0],[0,0,1]], initial = [0,1]
Output: 0
Example 2:
Input: graph = [[1,1,0],[1,1,1],[0,1,1]], initial = [0,1]
Output: 1
Example 3:
Input: graph = [[1,1,0,0],[1,1,1,0],[0,1,1,1],[0,0,1,1]], initial = [0,1]
Output: 1
Note:
1 < graph.length = graph[0].length <= 300
0 <= graph[i][j] == graph[j][i] <= 1
graph[i][i] = 1
1 <= initial.length < graph.length
0 <= initial[i] < graph.length
Solution
/**
*/
class Solution {
public int minMalwareSpread(int[][] graph, int[] initial) {
HashSet<Integer> malware = new HashSet<>();
int len = graph.length;
for (int init : initial) {
malware.add(init);
}
List<Integer>[] count = new List[len];
for (int i = 0; i < len; i++) {
count[i] = new ArrayList<Integer>();
}
for (int init : initial) {
Queue<Integer> queue = new LinkedList<>();
HashSet<Integer> visited = new HashSet<>();
queue.offer(init);
while (!queue.isEmpty()) {
int cur = queue.poll();
visited.add(cur);
count[cur].add(init);
for (int i = 0; i < len; i++) {
if (cur != i && graph[cur][i] == 1 && !malware.contains(i) && !visited.contains(i)) {
queue.offer(i);
}
}
}
}
int[] affectCount = new int[len];
for (int i = 0; i < len; i++) {
if (malware.contains(i) || count[i].size() != 1) {
continue;
}
affectCount[count[i].get(0)]++;
}
int res = -1;
int maxSize = 0;
Arrays.sort(initial);
for (int idx = 0; idx < len; idx++) {
if (affectCount[idx] > maxSize) {
maxSize = affectCount[idx];
res = idx;
}
}
if (maxSize == 0) {
return initial[0];
}
return res;
}
}
2020-06-15
560. Subarray Sum Equals K
Description
Given an array of integers and an integer k, you need to find the total number of continuous subarrays whose sum equals to k.
Example 1:
Input:nums = [1,1,1], k = 2
Output: 2
Constraints:
The length of the array is in range [1, 20,000].
The range of numbers in the array is [-1000, 1000] and the range of the integer k is [-1e7, 1e7].
Solution
class Solution {
public int subarraySum(int[] nums, int k) {
if(nums == null || nums.length == 0){
return 0;
}
HashMap<Integer,Integer> preSum = new HashMap();
preSum.put(0,1);
int res = 0, sum =0;
for(int i = 0;i<nums.length;i++){
int cur = nums[i];
sum+=cur;
if(preSum.containsKey(sum-k)){
res += preSum.get(sum-k);
}
preSum.put(sum,preSum.getOrDefault(sum,0)+1);
}
return res;
}
}
1074. Number of Submatrices That Sum to Target
Description
Given a matrix, and a target, return the number of non-empty submatrices that sum to target.
A submatrix x1, y1, x2, y2 is the set of all cells matrix[x][y] with x1 <= x <= x2 and y1 <= y <= y2.
Two submatrices (x1, y1, x2, y2) and (x1’, y1’, x2’, y2’) are different if they have some coordinate that is different: for example, if x1 != x1’.
Example 1:
Input: matrix = [[0,1,0],[1,1,1],[0,1,0]], target = 0
Output: 4
Explanation: The four 1x1 submatrices that only contain 0.
Example 2:
Input: matrix = [[1,-1],[-1,1]], target = 0
Output: 5
Explanation: The two 1x2 submatrices, plus the two 2x1 submatrices, plus the 2x2 submatrix.
Solution
class Solution {
public int numSubmatrixSumTarget(int[][] matrix, int target) {
HashMap<Integer, Integer> counter = new HashMap<>();
int res = 0;
int m = matrix.length, n = matrix[0].length;
//count the sum from matrix[i][0] to matrix[i][j]
for (int i = 0; i < m; i++) {
for (int j = 1; j < n; j++) {
matrix[i][j] += matrix[i][j - 1];
}
}
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
counter.clear();
counter.put(0, 1);
int cur = 0;
for (int[] ints : matrix) {
//sum from the top of matrix to current row
//where left = i and right = j.
cur += ints[j] - (i > 0 ? ints[i - 1] : 0);
//cur is from the top
//cur-target, means how many sub can sum to cur-target
//so the sum of sub and sub-cur will be (cur-target) + target = cur;
res += counter.getOrDefault(cur - target, 0);
counter.put(cur, counter.getOrDefault(cur, 0) + 1);
}
}
}
return res;
}
}
424. Longest Repeating Character Replacement
Description
Given a string s that consists of only uppercase English letters, you can perform at most k operations on that string.
In one operation, you can choose any character of the string and change it to any other uppercase English character.
Find the length of the longest sub-string containing all repeating letters you can get after performing the above operations.
Note: Both the string’s length and k will not exceed 104.
Example 1:
Input:
s = "ABAB", k = 2
Output:
4
Explanation:
Replace the two 'A's with two 'B's or vice versa.
Example 2:
Input:
s = "AABABBA", k = 1
Output:
4
Explanation:
Replace the one 'A' in the middle with 'B' and form "AABBBBA".
The substring "BBBB" has the longest repeating letters, which is 4.
Solution
better yet confusing O(n) solotion can be found here.
//count the number of char in the window
//if the total - maxCount is larger than K, means it's invalid
//that K moves will not make the window valid.
//so we keep moving left until the window is valid.
class Solution {
public int characterReplacement(String s, int k) {
int[] count = new int[26];
int left = 0, right = 0, maxLen = 0;
int len = s.length();
while (right < len) {
char chRight = s.charAt(right);
count[chRight - 'A']++;
int num_max = findMax(count);
while (right - left + 1 - num_max > k) {
count[s.charAt(left++) - 'A']--;
num_max = findMax(count);
}
maxLen = Math.max(maxLen, right - left + 1);
right++;
}
return maxLen;
}
public int findMax(int[] A) {
return Arrays.stream(A).max().getAsInt();
}
}
