- 2020-06-16
- 2020-06-17
- 2020-06-18
- 2020-06-19
- 2020-06-20
- 2020-06-21
- 2020-06-22
- 2020-06-23
- 2020-06-24
- 2020-06-25
- 2020-06-26
- 2020-06-27
- 2020-06-28
- 2020-06-29
- 2020-06-30
2020-06-16
480. Sliding Window Median
Description
Median is the middle value in an ordered integer list. If the size of the list is even, there is no middle value. So the median is the mean of the two middle value.
Examples:
[2,3,4] , the median is 3
[2,3], the median is (2 + 3) / 2 = 2.5
Given an array nums, there is a sliding window of size k which is moving from the very left of the array to the very right. You can only see the k numbers in the window. Each time the sliding window moves right by one position. Your job is to output the median array for each window in the original array.
For example,
Given nums = [1,3,-1,-3,5,3,6,7], and k = 3.
Window position Median
--------------- -----
[1 3 -1] -3 5 3 6 7 1
1 [3 -1 -3] 5 3 6 7 -1
1 3 [-1 -3 5] 3 6 7 -1
1 3 -1 [-3 5 3] 6 7 3
1 3 -1 -3 [5 3 6] 7 5
1 3 -1 -3 5 [3 6 7] 6
Therefore, return the median sliding window as [1,-1,-1,3,5,6].
Note:
You may assume k is always valid, ie: k is always smaller than input array's size for non-empty array.
Answers within 10^-5 of the actual value will be accepted as correct.
Solution
class Solution {
public double[] medianSlidingWindow(int[] nums, int k) {
Med med = new Med();
for (int i = 0; i < k; i++) {
med.push(nums[i]);
}
double[] res = new double[nums.length - k + 1];
int idx = 0;
res[idx++] = med.get();
for (int i = k; i < nums.length; i++) {
med.push(nums[i]);
med.pop(nums[i - k]);
res[idx++] = med.get();
}
return res;
}
//in order to compare int, Long is required
//in case of Integer.MAX_VALUE - Integer.MIN_VALUE is overflow.
class Med {
PriorityQueue<Long> smaller;
PriorityQueue<Long> larger;
public Med() {
//comparator should use Long.compareTo instead of simply (int)b-a
//in case of overflow.
smaller = new PriorityQueue<>((a, b) -> Long.compare(b, a));
larger = new PriorityQueue<>();
}
public void push(long num) {
smaller.offer(num);
larger.offer(smaller.poll());
//always keep smaller heap larger or equal
while (smaller.size() < larger.size()) {
smaller.offer(larger.poll());
}
}
public double get() {
if (smaller.size() == larger.size()) {
return ((double) smaller.peek() + (double) larger.peek()) / 2;
} else {
return (double) smaller.peek();
}
}
public void pop(long num) {
if (num >= larger.peek()) {
larger.remove(num);
//keep larger heap one or zero less than smaller.
larger.offer(smaller.poll());
} else {
smaller.remove(num);
}
while (smaller.size() < larger.size()) {
smaller.offer(larger.poll());
}
}
}
}
567. Permutation in String
Description
Given two strings s1 and s2, write a function to return true if s2 contains the permutation of s1. In other words, one of the first string’s permutations is the substring of the second string.
Example 1:
Input: s1 = "ab" s2 = "eidbaooo"
Output: True
Explanation: s2 contains one permutation of s1 ("ba").
Example 2:
Input:s1= "ab" s2 = "eidboaoo"
Output: False
Constraints:
The input strings only contain lower case letters.
The length of both given strings is in range [1, 10,000].
Solution
/**
1. How do we know string p is a permutation of string s? Easy, each character in p is in s too. So we can abstract all permutation strings of s to a map (Character -> Count). i.e. abba -> {a:2, b:2}. Since there are only 26 lower case letters in this problem, we can just use an array to represent the map.
2. How do we know string s2 contains a permutation of s1? We just need to create a sliding window with length of s1, move from beginning to the end of s2. When a character moves in from right of the window, we subtract 1 to that character count from the map. When a character moves out from left of the window, we add 1 to that character count. So once we see all zeros in the map, meaning equal numbers of every characters between s1 and the substring in the sliding window, we know the answer is true.
*/
class Solution {
public boolean checkInclusion(String s1, String s2) {
int[] count = new int[26];
int toFit = 0;
for (int i = 0; i < s1.length(); i++) {
count[s1.charAt(i) - 'a']++;
count[s2.charAt(i) - 'a']--;
}
for (int i = 0; i < 26; i++) {
if (count[i] > 0) {
toFit+=count[i];
}
}
if (toFit == 0) {
return true;
}
int len1 = s1.length();
//only char in s1 can have count[ch] > 0
for (int i = len1; i < s2.length(); i++) {
//some char in s1 pop out of window
if (++count[s2.charAt(i - len1) - 'a'] > 0) {
toFit++;
}
//some char in s1 just push in the window
if (count[s2.charAt(i) - 'a']-- > 0) {
toFit--;
}
if (toFit == 0) {
return true;
}
}
return false;
}
}
978. Longest Turbulent Subarray
Description
A subarray A[i], A[i+1], …, A[j] of A is said to be turbulent if and only if:
For i <= k < j, A[k] > A[k+1] when k is odd, and A[k] < A[k+1] when k is even; OR, for i <= k < j, A[k] > A[k+1] when k is even, and A[k] < A[k+1] when k is odd. That is, the subarray is turbulent if the comparison sign flips between each adjacent pair of elements in the subarray.
Return the length of a maximum size turbulent subarray of A.
Example 1:
Input: [9,4,2,10,7,8,8,1,9]
Output: 5
Explanation: (A[1] > A[2] < A[3] > A[4] < A[5])
Example 2:
Input: [4,8,12,16]
Output: 2
Example 3:
Input: [100]
Output: 1
Note:
1 <= A.length <= 40000
0 <= A[i] <= 10^9
Solution
class Solution {
public int maxTurbulenceSize(int[] A) {
int ins = 1, dec = 1;
int res = 1;
for (int i = 1; i < A.length; i++) {
//if increase
//previous one should be decrease.
//now descrease will be reset to 1.
if (A[i - 1] < A[i]) {
ins = dec + 1;
dec = 1;
} else if (A[i - 1] > A[i]) {
//if decrease
//previous one should be increase
//reset increase to one so if next one ois decrease
//dec = ins+1 = 2
dec = ins + 1;
ins = 1;
} else {
ins = 1;
dec = 1;
}
res = Math.max(res, Math.max(dec, ins));
}
return res;
}
}
1004. Max Consecutive Ones III
Description
Given an array A of 0s and 1s, we may change up to K values from 0 to 1.
Return the length of the longest (contiguous) subarray that contains only 1s.
Example 1:
Input: A = [1,1,1,0,0,0,1,1,1,1,0], K = 2
Output: 6
Explanation:
[1,1,1,0,0,1,1,1,1,1,1]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
Example 2:
Input: A = [0,0,1,1,0,0,1,1,1,0,1,1,0,0,0,1,1,1,1], K = 3
Output: 10
Explanation:
[0,0,1,1,1,1,1,1,1,1,1,1,0,0,0,1,1,1,1]
Bolded numbers were flipped from 0 to 1. The longest subarray is underlined.
Note:
1 <= A.length <= 20000
0 <= K <= A.length
A[i] is 0 or 1
Solution
class Solution {
public int longestOnes(int[] A, int K) {
int left = 0, right = 0;
int sum = 0;
int maxLen = 0;
while(right<A.length){
sum += A[right];
//gap is the total number of changes need to be made to make the window valid.
int gap = right - left + 1 -sum;
while(gap > K){
sum -= A[left++];
gap = right - left + 1 -sum;
}
maxLen = Math.max(maxLen,right-left+1);
right++;
}
return maxLen;
}
}
241. Different Ways to Add Parentheses
Description
Given a string of numbers and operators, return all possible results from computing all the different possible ways to group numbers and operators. The valid operators are +, - and *.
Example 1:
Input: “2-1-1” Output: [0, 2] Explanation: ((2-1)-1) = 0 (2-(1-1)) = 2 Example 2:
Input: “2*3-4*5” Output: [-34, -14, -10, -10, 10] Explanation: (2*(3-(4*5))) = -34 ((2*3)-(4*5)) = -14 ((2*(3-4))*5) = -10 (2*((3-4)*5)) = -10 (((2*3)-4)*5) = 10
Solution
/**
Divide and Conqur
if the current position is a character (+-*), then try to solve substring of it's side.
*/
class Solution {
public List<Integer> diffWaysToCompute(String input) {
List<Integer> res = new ArrayList<>();
for (int i = 0; i < input.length(); i++) {
char c = input.charAt(i);
if (c == '+' || c == '-' || c == '*') {
//all possible value can be achieved from left
List<Integer> res_a = diffWaysToCompute(input.substring(0, i));
//all possible value can be achieved from right
List<Integer> res_b = diffWaysToCompute(input.substring(i + 1));
//combine all values together
for (int a : res_a) {
for (int b : res_b) {
switch (c) {
case '+':
res.add(a + b);
break;
case '-':
res.add(a - b);
break;
case '*':
res.add(a * b);
break;
default:
break;
}
}
}
}
}
if (res.isEmpty()) {
res.add(Integer.parseInt(input));
}
return res;
}
}
2020-06-17
938. Range Sum of BST
Description
Given the root node of a binary search tree, return the sum of values of all nodes with value between L and R (inclusive).
The binary search tree is guaranteed to have unique values.
Example 1:
Input: root = [10,5,15,3,7,null,18], L = 7, R = 15
Output: 32
Example 2:
Input: root = [10,5,15,3,7,13,18,1,null,6], L = 6, R = 10
Output: 23
Note:
The number of nodes in the tree is at most 10000.
The final answer is guaranteed to be less than 2^31.
Solution
class Solution {
public int rangeSumBST(TreeNode root, int L, int R) {
if (root == null) {
return 0;
}
int val = (root.val >= L && root.val <= R) ? root.val : 0;
return val+rangeSumBST(root.left, L, R) + rangeSumBST(root.right, L, R);
}
}
2020-06-18
894. All Possible Full Binary Trees
Description
A full binary tree is a binary tree where each node has exactly 0 or 2 children.
Return a list of all possible full binary trees with N nodes. Each element of the answer is the root node of one possible tree.
Each node of each tree in the answer must have node.val = 0.
You may return the final list of trees in any order.
Example 1:
Input: 7
Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]
Explanation:
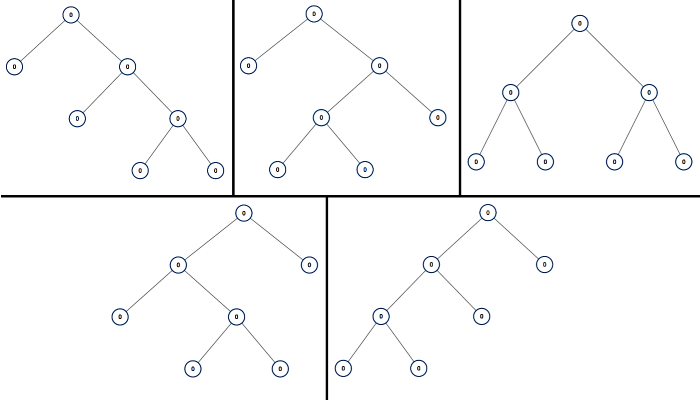
Solution
class Solution {
Map<Integer, List<TreeNode>> memo = new HashMap<>();
public List<TreeNode> allPossibleFBT(int N) {
if (memo.containsKey(N)) {
return memo.get(N);
}
List<TreeNode> res = new ArrayList<>();
if (N == 1) {
res.add(new TreeNode(0));
return res;
}
if (N % 2 == 0) {
return res;
}
for (int i = 1; i < N; i += 2) {
List<TreeNode> leftPart = allPossibleFBT(i);
List<TreeNode> rightPart = allPossibleFBT(N - i - 1);
for (TreeNode leftNode : leftPart) {
for (TreeNode rightNode : rightPart) {
TreeNode temp = new TreeNode(0);
temp.left = leftNode;
temp.right = rightNode;
res.add(temp);
}
}
}
memo.put(N, res);
return res;
}
}
687. Longest Univalue Path
Description
Given a binary tree, find the length of the longest path where each node in the path has the same value. This path may or may not pass through the root.
The length of path between two nodes is represented by the number of edges between them.
Example 1:
Input:
5
/ \
4 5
/ \ \
1 1 5
Output: 2
Example 2:
Input:
1
/ \
4 5
/ \ \
4 4 5
Output: 2
Note: The given binary tree has not more than 10000 nodes. The height of the tree is not more than 1000.
Solution
class Solution {
int max_len;
public int longestUnivaluePath(TreeNode root) {
if(root == null) return 0;
max_len = 0;
getMax_len(root,root.val);
return max_len;
}
private int getMax_len(TreeNode root, int val) {
if (root == null) {
return 0;
}
int left_len = getMax_len(root.left, root.val);
int right_len = getMax_len(root.right, root.val);
//find the max length of path from left to root to right
max_len = Math.max(max_len, left_len + right_len);
//if the current node can form a path top down
if (val == root.val) {
return Math.max(left_len, right_len) + 1;
}
//if the current value is different from its parent, unable to form a path.
return 0;
}
}
726. Number of Atoms
Description
Given a chemical formula (given as a string), return the count of each atom.
An atomic element always starts with an uppercase character, then zero or more lowercase letters, representing the name.
1 or more digits representing the count of that element may follow if the count is greater than 1. If the count is 1, no digits will follow. For example, H2O and H2O2 are possible, but H1O2 is impossible.
Two formulas concatenated together produce another formula. For example, H2O2He3Mg4 is also a formula.
A formula placed in parentheses, and a count (optionally added) is also a formula. For example, (H2O2) and (H2O2)3 are formulas.
Given a formula, output the count of all elements as a string in the following form: the first name (in sorted order), followed by its count (if that count is more than 1), followed by the second name (in sorted order), followed by its count (if that count is more than 1), and so on.
Example 1:
Input:
formula = "H2O"
Output: "H2O"
Explanation:
The count of elements are {'H': 2, 'O': 1}.
Example 2:
Input:
formula = "Mg(OH)2"
Output: "H2MgO2"
Explanation:
The count of elements are {'H': 2, 'Mg': 1, 'O': 2}.
Example 3:
Input:
formula = "K4(ON(SO3)2)2"
Output: "K4N2O14S4"
Explanation:
The count of elements are {'K': 4, 'N': 2, 'O': 14, 'S': 4}.
Note:
All atom names consist of lowercase letters, except for the first character which is uppercase.
The length of formula will be in the range [1, 1000].
formula will only consist of letters, digits, and round parentheses, and is a valid formula as defined in the problem.
Solution
class Solution {
public String countOfAtoms(String formula) {
Stack<Map<String, Integer>> stack = new Stack<>();
Map<String, Integer> map = new HashMap<>();
int i = 0, n = formula.length();
while (i < n) {
char c = formula.charAt(i);
i++;
if (c == '(') {
stack.push(map);
map = new HashMap<>();
} else if (c == ')') {
int val = 0;
while (i < n && Character.isDigit(formula.charAt(i))) {
val = val * 10 + formula.charAt(i++) - '0';
}
if (val == 0) {
val = 1;
}
if (!stack.isEmpty()) {
Map<String, Integer> temp = map;
map = stack.pop();
for (String key : temp.keySet()) {
map.put(key, map.getOrDefault(key, 0) + temp.get(key) * val);
}
}
} else {
int start = i - 1;
while (i < n && Character.isLowerCase(formula.charAt(i))) {
i++;
}
String s = formula.substring(start, i);
int val = 0;
while (i < n && Character.isDigit(formula.charAt(i))) {
val = val * 10 + formula.charAt(i++) - '0';
}
if (val == 0) {
val = 1;
}
map.put(s, map.getOrDefault(s, 0) + val);
}
}
StringBuilder sb = new StringBuilder();
List<String> list = new ArrayList<>(map.keySet());
Collections.sort(list);
for (String key : list) {
sb.append(key);
if (map.get(key) > 1) {
sb.append(map.get(key));
}
}
return sb.toString();
}
}
247. Strobogrammatic Number II
Description
A strobogrammatic number is a number that looks the same when rotated 180 degrees (looked at upside down).
Find all strobogrammatic numbers that are of length = n.
Example:
Input: n = 2
Output: ["11","69","88","96"]
Solution
class Solution {
public List<String> findStrobogrammatic(int n) {
return helper(n, n);
}
List<String> helper(int n, int m) {
if (n == 0) return new ArrayList<String>(Collections.singletonList(""));
if (n == 1) return new ArrayList<String>(Arrays.asList("0", "1", "8"));
List<String> list = helper(n - 2, m);
List<String> res = new ArrayList<String>();
for (int i = 0; i < list.size(); i++) {
String s = list.get(i);
if (n != m) res.add("0" + s + "0");
res.add("1" + s + "1");
res.add("6" + s + "9");
res.add("8" + s + "8");
res.add("9" + s + "6");
}
return res;
}
}
783. Minimum Distance Between BST Nodes
Description
Given a Binary Search Tree (BST) with the root node root, return the minimum difference between the values of any two different nodes in the tree.
Example :
Input: root = [4,2,6,1,3,null,null]
Output: 1
Explanation:
Note that root is a TreeNode object, not an array.
The given tree [4,2,6,1,3,null,null] is represented by the following diagram:
4
/ \
2 6
/ \
1 3
while the minimum difference in this tree is 1, it occurs between node 1 and node 2, also between node 3 and node 2.
Note:
The size of the BST will be between 2 and 100.
Solution
class Solution {
public int getMinimumDifference(TreeNode root) {
//// contains at most 1 value to store the previous value.
List<Integer> prev = new ArrayList<>();
//use to store global min.
int[] min = new int[]{Integer.MAX_VALUE};
inorder(root, prev, min);
return min[0];
}
private void inorder(TreeNode root, List<Integer> prev, int[] min) {
if (root == null) {
return;
}
inorder(root.left, prev, min);
if (prev.isEmpty()) {
prev.add(root.val);
} else {
min[0] = Math.min(min[0], Math.abs(root.val - prev.get(0)));
prev.set(0, root.val);
}
inorder(root.right, prev, min);
}
}
776. Split BST
Description
Given a Binary Search Tree (BST) with root node root, and a target value V, split the tree into two subtrees where one subtree has nodes that are all smaller or equal to the target value, while the other subtree has all nodes that are greater than the target value. It’s not necessarily the case that the tree contains a node with value V.
Additionally, most of the structure of the original tree should remain. Formally, for any child C with parent P in the original tree, if they are both in the same subtree after the split, then node C should still have the parent P.
You should output the root TreeNode of both subtrees after splitting, in any order.
Example 1:
Input: root = [4,2,6,1,3,5,7], V = 2
Output: [[2,1],[4,3,6,null,null,5,7]]
Explanation:
Note that root, output[0], and output[1] are TreeNode objects, not arrays.
The given tree [4,2,6,1,3,5,7] is represented by the following diagram:
4
/ \
2 6
/ \ / \
1 3 5 7
while the diagrams for the outputs are:
4
/ \
3 6 and 2
/ \ /
5 7 1
Note:
The size of the BST will not exceed 50.
The BST is always valid and each node's value is different.
Solution
class Solution {
public TreeNode[] splitBST(TreeNode root, int V) {
TreeNode[] res = new TreeNode[]{null, null};
if (root == null) {
return res;
}
//cur ont the right side.
if (root.val <= V) {
//root will be the smaller one.
res[0] = root;
//split root.right
TreeNode[] rightSide = splitBST(root.right, V);
//rightSide[0] will be the smaller part which smaller than V
//append to root.right.
root.right = rightSide[0];
//rightSide[1] are nodes larger than V.
//be a separate one.
res[1] = rightSide[1];
} else {
res[1] = root;
TreeNode[] leftSide = splitBST(root.left, V);
root.left = leftSide[1];
res[0] = leftSide[0];
}
return res;
}
}
2020-06-19
779. K-th Symbol in Grammar
Description
On the first row, we write a 0. Now in every subsequent row, we look at the previous row and replace each occurrence of 0 with 01, and each occurrence of 1 with 10.
Given row N and index K, return the K-th indexed symbol in row N. (The values of K are 1-indexed.) (1 indexed).
Examples:
Input: N = 1, K = 1
Output: 0
Input: N = 2, K = 1
Output: 0
Input: N = 2, K = 2
Output: 1
Input: N = 4, K = 5
Output: 1
Explanation:
row 1: 0
row 2: 01
row 3: 0110
row 4: 01101001
Note:
N will be an integer in the range [1, 30].
K will be an integer in the range [1, 2^(N-1)].
Solution
class Solution {
public int kthGrammar(int N, int K) {
if (N == 1) {
return 0;
}
if (K % 2 == 0) {
return Math.abs(-(kthGrammar(N - 1, K / 2) - 1));
} else {
return kthGrammar(N - 1, (K + 1) / 2);
}
}
}
2020-06-20
219. Contains Duplicate II
Description
Given an array of integers and an integer k, find out whether there are two distinct indices i and j in the array such that nums[i] = nums[j] and the absolute difference between i and j is at most k.
Example 1:
Input: nums = [1,2,3,1], k = 3
Output: true
Example 2:
Input: nums = [1,0,1,1], k = 1
Output: true
Example 3:
Input: nums = [1,2,3,1,2,3], k = 2
Output: false
Solution
//use map to store the index of the previous equal number.
class Solution {
public boolean containsNearbyDuplicate(int[] nums, int k) {
HashMap<Integer,Integer> map = new HashMap();
for(int i=0;i<nums.length;i++){
int num = nums[i];
if(map.containsKey(num)){
if(i-map.get(num)<=k){
return true;
}
}
map.put(num,i);
}
return false;
}
}
220. Contains Duplicate III
Description
Given an array of integers, find out whether there are two distinct indices i and j in the array such that the absolute difference between nums[i] and nums[j] is at most t and the absolute difference between i and j is at most k.
Example 1:
Input: nums = [1,2,3,1], k = 3, t = 0
Output: true
Example 2:
Input: nums = [1,0,1,1], k = 1, t = 2
Output: true
Example 3:
Input: nums = [1,5,9,1,5,9], k = 2, t = 3
Output: false
Solution
//KEY POINT: use long to prevent overflow.
//main idea is to use butket to prevent loop over all possible value [i-t,i+t]
//instead just use bucket to store it.
public class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
if (k < 1 || t < 0) {
return false;
}
Map<Long, Long> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
long numL = (long)nums[i]+ Integer.MAX_VALUE;
long bucket = numL / ((long) t + 1);
if ((map.containsKey(bucket)) ||
(map.containsKey(bucket - 1) && numL - map.get(bucket - 1) <= t) ||
(map.containsKey(bucket + 1) && map.get(bucket + 1) - numL <= t)
) {
return true;
}
if (map.size() >= k) {
long preBucket = ((long) nums[i - k]+ Integer.MAX_VALUE) / ((long)t + 1);
map.remove(preBucket);
}
map.put(bucket, numL);
}
return false;
}
}
class Solution {
public boolean containsNearbyAlmostDuplicate(int[] nums, int k, int t) {
if(nums == null || nums.length < 2 || k < 1) return false;
TreeSet<Long> set = new TreeSet<>();
for(int i = 0; i < nums.length; i++){
long l = (long) nums[i];
//floor: Returns the greatest element in this set less than or equal to the given element, or null if there is no such element.
Long floor = set.floor(l);
//Ceiling: Returns the least element in this set greater than or equal to the given element, or null if there is no such element.
Long ceil = set.ceiling(l);
// the tricky part I modified to easily understood way.
if((floor != null && l - floor <= t) ||
(ceil != null && ceil - l <= t) )
return true;
set.add(l);
if(i >= k)
set.remove((long)nums[i -k]);
}
return false;
}
}
352. Data Stream as Disjoint Intervals
Description
Given a data stream input of non-negative integers a1, a2, …, an, …, summarize the numbers seen so far as a list of disjoint intervals.
For example, suppose the integers from the data stream are 1, 3, 7, 2, 6, ..., then the summary will be:
[1, 1]
[1, 1], [3, 3]
[1, 1], [3, 3], [7, 7]
[1, 3], [7, 7]
[1, 3], [6, 7]
Follow up:
What if there are lots of merges and the number of disjoint intervals are small compared to the data stream's size?
Solution
/**
Four situation:
1. [...,VAL-1]VAL[VAL+1,...] -> merge two intervals
2. [...,VAL-1]VAL ... [VAL+x,...] -> merge lower interval
3. [...,VAL-x] ... VAL[VAL+1,...] -> merge highrer interval
4. [...,VAL-x] ... VAL ... [VAL+x,...] -> create a new interval only contains val.
*/
class SummaryRanges {
TreeMap<Integer, int[]> tree;
/**
* Initialize your data structure here.
*/
public SummaryRanges() {
tree = new TreeMap<>();
}
public void addNum(int val) {
if (tree.containsKey(val)) {
return;
}
Integer L = tree.lowerKey(val);
Integer H = tree.higherKey(val);
if (L != null && H != null && tree.get(L)[1] == val - 1 && H == val + 1) {
//1. [...,VAL-1]VAL[VAL+1,...] -> merge two intervals
tree.get(L)[1] = tree.get(H)[1];
tree.remove(H);
} else if (L != null && val <= tree.get(L)[1]+1) {
//2. [...,VAL-1]VAL ... [VAL+x,...] -> merge lower interval
tree.get(L)[1] = Math.max(tree.get(L)[1], val);
} else if (H != null && tree.get(H)[0] == val + 1) {
//3. [...,VAL-x] ... VAL[VAL+1,...] -> merge highrer interval
tree.put(val, new int[]{val, tree.get(H)[1]});
tree.remove(H);
} else {
//4. [...,VAL-x] ... VAL ... [VAL+x,...] -> create a new interval only contains val.
tree.put(val, new int[]{val, val});
}
}
public int[][] getIntervals() {
int size = tree.size();
int[][] res = new int[size][2];
Iterator<int[]> iter = tree.values().iterator();
int idx = 0;
while(iter.hasNext()){
res[idx++] = iter.next();
}
return res;
}
}
729. My Calendar I
Description
Implement a MyCalendar class to store your events. A new event can be added if adding the event will not cause a double booking.
Your class will have the method, book(int start, int end). Formally, this represents a booking on the half open interval [start, end), the range of real numbers x such that start <= x < end.
A double booking happens when two events have some non-empty intersection (ie., there is some time that is common to both events.)
For each call to the method MyCalendar.book, return true if the event can be added to the calendar successfully without causing a double booking. Otherwise, return false and do not add the event to the calendar.
Your class will be called like this: MyCalendar cal = new MyCalendar(); MyCalendar.book(start, end)
Example 1:
MyCalendar();
MyCalendar.book(10, 20); // returns true
MyCalendar.book(15, 25); // returns false
MyCalendar.book(20, 30); // returns true
Explanation:
The first event can be booked. The second can't because time 15 is already booked by another event.
The third event can be booked, as the first event takes every time less than 20, but not including 20.
Note:
The number of calls to MyCalendar.book per test case will be at most 1000.
In calls to MyCalendar.book(start, end), start and end are integers in the range [0, 10^9].
Solution
import java.util.TreeMap;
class MyCalendar {
TreeMap<Integer, int[]> calendar;
public MyCalendar() {
calendar = new TreeMap<>();
}
public boolean book(int start, int end) {
if (calendar.containsKey(start)) {
return false;
}
Integer before = calendar.lowerKey(start);
Integer after = calendar.higherKey(start);
//only one situation is valid:
//before: either not exist or end is smaller than start
//after: either not exist or start is larger than end.
if ((before == null || (calendar.get(before)[1] < start)) &&
(after == null || calendar.get(after)[0] > end - 1)
) {
calendar.put(start, new int[]{start, end - 1});
return true;
}
return false;
}
}
731. My Calendar II
Description
Implement a MyCalendarTwo class to store your events. A new event can be added if adding the event will not cause a triple booking.
Your class will have one method, book(int start, int end). Formally, this represents a booking on the half open interval [start, end), the range of real numbers x such that start <= x < end.
A triple booking happens when three events have some non-empty intersection (ie., there is some time that is common to all 3 events.)
For each call to the method MyCalendar.book, return true if the event can be added to the calendar successfully without causing a triple booking. Otherwise, return false and do not add the event to the calendar.
Your class will be called like this: MyCalendar cal = new MyCalendar(); MyCalendar.book(start, end)
Example 1:
MyCalendar();
MyCalendar.book(10, 20); // returns true
MyCalendar.book(50, 60); // returns true
MyCalendar.book(10, 40); // returns true
MyCalendar.book(5, 15); // returns false
MyCalendar.book(5, 10); // returns true
MyCalendar.book(25, 55); // returns true
Explanation:
The first two events can be booked. The third event can be double booked.
The fourth event (5, 15) can't be booked, because it would result in a triple booking.
The fifth event (5, 10) can be booked, as it does not use time 10 which is already double booked.
The sixth event (25, 55) can be booked, as the time in [25, 40) will be double booked with the third event;
the time [40, 50) will be single booked, and the time [50, 55) will be double booked with the second event.
Note:
The number of calls to MyCalendar.book per test case will be at most 1000.
In calls to MyCalendar.book(start, end), start and end are integers in the range [0, 10^9].
Solution
/**
Use TreeMap to store the information/count of start and end.
for each start, +1, each end -1.
so the count will be the overlap right now.
go through the map and check whether overlap exceed 2.
MUST use TreeMap so the entrySet will be ordered, otherwise the overlap count is not correct.
*/
class MyCalendarTwo {
Map<Integer, Integer> calendar;
public MyCalendarTwo() {
calendar = new TreeMap<>();
}
public boolean book(int start, int end) {
//add it to map to check validation.
calendar.put(start, calendar.getOrDefault(start, 0) + 1);
calendar.put(end, calendar.getOrDefault(end, 0) - 1);
int count = 0;
for (Map.Entry<Integer, Integer> entry : calendar.entrySet()) {
count += entry.getValue();
//if not valid, need to remove both start and end.
if(count > 2){
calendar.put(start, calendar.get(start) - 1);
if(calendar.get(start)==0){
calendar.remove(start);
}
calendar.put(end, calendar.get(end) + 1);
if(calendar.get(end)==0){
calendar.remove(end);
}
return false;
}
}
return true;
}
}
/**
* Your MyCalendarTwo object will be instantiated and called as such: MyCalendarTwo obj = new MyCalendarTwo(); boolean param_1 = obj.book(start,end);
*/
732. My Calendar III
Description
Implement a MyCalendarThree class to store your events. A new event can always be added.
Your class will have one method, book(int start, int end). Formally, this represents a booking on the half open interval [start, end), the range of real numbers x such that start <= x < end.
A K-booking happens when K events have some non-empty intersection (ie., there is some time that is common to all K events.)
For each call to the method MyCalendar.book, return an integer K representing the largest integer such that there exists a K-booking in the calendar.
Your class will be called like this: MyCalendarThree cal = new MyCalendarThree(); MyCalendarThree.book(start, end)
Example 1:
MyCalendarThree();
MyCalendarThree.book(10, 20); // returns 1
MyCalendarThree.book(50, 60); // returns 1
MyCalendarThree.book(10, 40); // returns 2
MyCalendarThree.book(5, 15); // returns 3
MyCalendarThree.book(5, 10); // returns 3
MyCalendarThree.book(25, 55); // returns 3
Explanation:
The first two events can be booked and are disjoint, so the maximum K-booking is a 1-booking.
The third event [10, 40) intersects the first event, and the maximum K-booking is a 2-booking.
The remaining events cause the maximum K-booking to be only a 3-booking.
Note that the last event locally causes a 2-booking, but the answer is still 3 because
eg. [10, 20), [10, 40), and [5, 15) are still triple booked.
Note:
The number of calls to MyCalendarThree.book per test case will be at most 400.
In calls to MyCalendarThree.book(start, end), start and end are integers in the range [0, 10^9].
Solution
/**
Maintain a treemap that store the info:<idx,count>
means the overlap count after idx(and before next idx)
*/
class MyCalendarThree {
TreeMap<Integer, Integer> treemap = new TreeMap<>();
int k = 0;
public MyCalendarThree() {
}
public int book(int start, int end) {
//if the map is empty.
if(treemap.size()==0){
treemap.put(start, 1);
treemap.put(end, 0);
k = 1;
return k;
}
//previous key than start
Integer pre_key = treemap.floorKey(start);
if(pre_key!=null){
//start will be one more overlap than the previous one.
treemap.put(start, treemap.get(pre_key)+1);
k = Math.max(treemap.get(start), k);
}else{
//if start is the smallest one.
treemap.put(start, 1);
k = Math.max(1, k);
}
Integer next_key = treemap.higherKey(start);
//nodes between start and end, each of them will increament by one.
while(next_key!=null && next_key<end){
int pre_count = treemap.get(next_key);
treemap.put(next_key, pre_count+1);
k = Math.max(k, pre_count+1);
next_key = treemap.higherKey(next_key);
}
//deal with the end.
pre_key = treemap.floorKey(end);
//end is one less than the previous key as the overlap ended.
if(pre_key<end){
treemap.put(end, treemap.get(pre_key)-1);
}
return k;
}
}
/**
* Your MyCalendarThree object will be instantiated and called as such:
* MyCalendarThree obj = new MyCalendarThree();
* int param_1 = obj.book(start,end);
*/
2020-06-21
683. K Empty Slots
Description
You have N bulbs in a row numbered from 1 to N. Initially, all the bulbs are turned off. We turn on exactly one bulb everyday until all bulbs are on after N days.
You are given an array bulbs of length N where bulbs[i] = x means that on the (i+1)th day, we will turn on the bulb at position x where i is 0-indexed and x is 1-indexed.
Given an integer K, find out the minimum day number such that there exists two turned on bulbs that have exactly K bulbs between them that are all turned off.
If there isn’t such day, return -1.
Example 1:
Input:
bulbs: [1,3,2]
K: 1
Output: 2
Explanation:
On the first day: bulbs[0] = 1, first bulb is turned on: [1,0,0]
On the second day: bulbs[1] = 3, third bulb is turned on: [1,0,1]
On the third day: bulbs[2] = 2, second bulb is turned on: [1,1,1]
We return 2 because on the second day, there were two on bulbs with one off bulb between them.
Example 2:
Input:
bulbs: [1,2,3]
K: 1
Output: -1
Solution
/**
* The idea is to use an array days[] to record each position's flower's blooming day.
* That means days[i] is the blooming day of the flower in position i+1.
* We just need to find a subarray days[left, left+1,..., left+k-1, right]
* which satisfies: for any i = left+1,..., left+k-1,
* we can have days[left] < days[i] && days[right] < days[i].
* Then, the result is max(days[left], days[right]).
*
*/
class Solution {
public int kEmptySlots(int[] flowers, int k) {
int[] days = new int[flowers.length];
for (int i = 0; i < flowers.length; i++) {
days[flowers[i] - 1] = i + 1;
}
int left = 0, right = k + 1, res = Integer.MAX_VALUE;
for (int i = 0; right < days.length; i++) {
//days[i] > days[left] && days[i] > days[right] is the only condition for i valid.
//if invalid, will move left and right to current position to find next position.
if (days[i] < days[left] || days[i] <= days[right]) {
//if i == right, means previous are all valid and reached the end.
if (i == right) {
res = Math.min(res, Math.max(days[left], days[right]));
//we get a valid subarray
}
//move left and right to a new place.
left = i;
right = k + 1 + i;
}
}
return (res == Integer.MAX_VALUE) ? -1 : res;
}
}
Another approach using treemap or other sorted datastructure.
class Solution {
public int kEmptySlots(int[] flowers, int k) {
TreeSet<Integer> active = new TreeSet();
int day = 0;
for (int flower : flowers) {
day++;
active.add(flower);
Integer lower = active.lower(flower)
Integer higher = active.higher(flower);
if (lower != null && flower - lower - 1 == k ||
higher != null && higher - flower - 1 == k) {
return day;
}
}
return -1;
}
}
715. Range Module
Description
A Range Module is a module that tracks ranges of numbers. Your task is to design and implement the following interfaces in an efficient manner.
addRange(int left, int right) Adds the half-open interval [left, right), tracking every real number in that interval. Adding an interval that partially overlaps with currently tracked numbers should add any numbers in the interval [left, right) that are not already tracked. queryRange(int left, int right) Returns true if and only if every real number in the interval [left, right) is currently being tracked. removeRange(int left, int right) Stops tracking every real number currently being tracked in the interval [left, right).
Example 1:
addRange(10, 20): null
removeRange(14, 16): null
queryRange(10, 14): true (Every number in [10, 14) is being tracked)
queryRange(13, 15): false (Numbers like 14, 14.03, 14.17 in [13, 15) are not being tracked)
queryRange(16, 17): true (The number 16 in [16, 17) is still being tracked, despite the remove operation)
Note:
A half open interval [left, right) denotes all real numbers left <= x < right.
0 < left < right < 10^9 in all calls to addRange, queryRange, removeRange.
The total number of calls to addRange in a single test case is at most 1000.
The total number of calls to queryRange in a single test case is at most 5000.
The total number of calls to removeRange in a single test case is at most 1000.
Solution
class RangeModule {
private TreeMap<Integer, Integer> map = new TreeMap<>();
public void addRange(int left, int right) {
if (left >= right) {
return;
}
Integer start = map.floorKey(left);
//if no previous interval
if (start == null) {
start = map.ceilingKey(left);
}
//go through all possible intervals and remove them.
while (start != null && start <= right) {
int end = map.get(start);
//if there exist interval
if (end >= left) {
map.remove(start);
//go left as far as possible
if (start < left) {
left = start;
}
//go right far possible.
if (end > right) {
right = end;
}
}
//go to next interval.
start = map.ceilingKey(end);
}
map.put(left, right);
}
public boolean queryRange(int left, int right) {
//find previous interval less or equals to left.
Integer floor = map.floorKey(left);
return floor != null && map.get(floor) >= right;
}
public void removeRange(int left, int right) {
if (left >= right) {
return;
}
Integer start = map.floorKey(left);
if (start == null) {
start = map.ceilingKey(left);
}
while (start != null && start < right) {
int end = map.get(start);
//if exist interval
if (end >= left) {
map.remove(start);
if (start < left) {
map.put(start, left);
}
if (end > right) {
map.put(right, end);
}
}
start = map.ceilingKey(end);
}
}
}
2020-06-22
621. Task Scheduler
Description
You are given a char array representing tasks CPU need to do. It contains capital letters A to Z where each letter represents a different task. Tasks could be done without the original order of the array. Each task is done in one unit of time. For each unit of time, the CPU could complete either one task or just be idle.
However, there is a non-negative integer n that represents the cooldown period between two same tasks (the same letter in the array), that is that there must be at least n units of time between any two same tasks.
You need to return the least number of units of times that the CPU will take to finish all the given tasks.
Example 1:
Input: tasks = ["A","A","A","B","B","B"], n = 2
Output: 8
Explanation:
A -> B -> idle -> A -> B -> idle -> A -> B
There is at least 2 units of time between any two same tasks.
Example 2:
Input: tasks = ["A","A","A","B","B","B"], n = 0
Output: 6
Explanation: On this case any permutation of size 6 would work since n = 0.
["A","A","A","B","B","B"]
["A","B","A","B","A","B"]
["B","B","B","A","A","A"]
...
And so on.
Example 3:
Input: tasks = ["A","B","C","D","E","A","B","C","D","E"], n = 4
Output: 10
Constraints:
The number of tasks is in the range [1, 10000].
The integer n is in the range [0, 100].
Solution
//Main idea is that the idle can be created only by task that have the most count.
//because if the taks with most count can be arranged, the less count task can simply append to it and will always be valid.
class Solution {
public int leastInterval(char[] tasks, int n) {
int[] count = new int[26];
int max = 0, max_count = 0;
for (char ch : tasks) {
count[ch - 'A']++;
max = Math.max(count[ch - 'A'], max);
}
for (int i = 0; i < 26; i++) {
if (count[i] == max) {
max_count++;
}
}
int gapCount = max - 1;
int emptySlot = gapCount * (n - (max_count - 1));
int availableTask = tasks.length - max_count * max;
int idle = Math.max(0, emptySlot - availableTask);
return tasks.length + idle;
}
}
363. Max Sum of Rectangle No Larger Than K
Description
Given a non-empty 2D matrix matrix and an integer k, find the max sum of a rectangle in the matrix such that its sum is no larger than k.
Example:
Input: matrix = [[1,0,1],[0,-2,3]], k = 2
Output: 2
Explanation: Because the sum of rectangle [[0, 1], [-2, 3]] is 2,
and 2 is the max number no larger than k (k = 2).
Note:
The rectangle inside the matrix must have an area > 0.
What if the number of rows is much larger than the number of columns?
Solution
class Solution {
public int maxSumSubmatrix(int[][] matrix, int k) {
TreeSet<Integer> counter = new TreeSet<>();
int res = Integer.MIN_VALUE;
int m = matrix.length, n = matrix[0].length;
//count the sum from matrix[i][0] to matrix[i][j]
for (int i = 0; i < m; i++) {
for (int j = 1; j < n; j++) {
matrix[i][j] += matrix[i][j - 1];
}
}
for (int i = 0; i < n; i++) {
for (int j = i; j < n; j++) {
counter.clear();
counter.add(0);
int cur = 0;
for (int[] ints : matrix) {
//sum from the top of matrix to current row
//where left = i and right = j.
cur += ints[j] - (i > 0 ? ints[i - 1] : 0);
//cur is from the top
//cur-target, means how many sub can sum to cur-target
//so the sum of sub and sub-cur will be (cur-target) + target = cur;
Integer temp = counter.ceiling(cur - k);
if (temp != null) {
res = Math.max(res, cur - temp);
} else if (cur <= k) {
res = Math.max(res, cur);
}
counter.add(cur);
}
}
}
return res;
}
}
933. Number of Recent Calls
Description
Write a class RecentCounter to count recent requests.
It has only one method: ping(int t), where t represents some time in milliseconds.
Return the number of pings that have been made from 3000 milliseconds ago until now.
Any ping with time in [t - 3000, t] will count, including the current ping.
It is guaranteed that every call to ping uses a strictly larger value of t than before.
Example 1:
Input: inputs = ["RecentCounter","ping","ping","ping","ping"], inputs = [[],[1],[100],[3001],[3002]]
Output: [null,1,2,3,3]
Note:
Each test case will have at most 10000 calls to ping.
Each test case will call ping with strictly increasing values of t.
Each call to ping will have 1 <= t <= 10^9.
Solution
class RecentCounter {
Queue<Integer> q;
public RecentCounter() {
q = new LinkedList<>();
}
public int ping(int t) {
q.offer(t);
while (q.peek() < t - 3000) { q.poll(); }
return q.size();
}
}
862. Shortest Subarray with Sum at Least K
Description
Return the length of the shortest, non-empty, contiguous subarray of A with sum at least K.
If there is no non-empty subarray with sum at least K, return -1.
Example 1:
Input: A = [1], K = 1
Output: 1
Example 2:
Input: A = [1,2], K = 4
Output: -1
Example 3:
Input: A = [2,-1,2], K = 3
Output: 3
Note:
1 <= A.length <= 50000
-10 ^ 5 <= A[i] <= 10 ^ 5
1 <= K <= 10 ^ 9
Solution
/**
How to think of such solutions?
Basic idea, for array starting at every A[i], find the shortest one with sum at leat K.
In my solution, for B[i], find the smallest j that B[j] - B[i] >= K.
Keep this in mind for understanding two while loops.
What is the purpose of first while loop?
For the current prefix sum B[i], it covers all subarray ending at A[i-1].
We want know if there is a subarray, which starts from an index, ends at A[i-1] and has at least sum K.
So we start to compare B[i] with the smallest prefix sum in our deque, which is B[D[0]], hoping that [i] - B[d[0]] >= K.
So if B[i] - B[d[0]] >= K, we can update our result res = min(res, i - d.popleft()).
The while loop helps compare one by one, until this condition isn't valid anymore.
Why we pop left in the first while loop?
This the most tricky part that improve my solution to get only O(N).
D[0] exists in our deque, it means that before B[i], we didn't find a subarray whose sum at least K.
B[i] is the first prefix sum that valid this condition.
In other words, A[D[0]] ~ A[i-1] is the shortest subarray starting at A[D[0]] with sum at least K.
We have already find it for A[D[0]] and it can't be shorter, so we can drop it from our deque.
What is the purpose of second while loop?
To keep B[D[i]] increasing in the deque.
Why keep the deque increase?
If B[i] <= B[d.back()] and moreover we already know that i > d.back(), it means that compared with d.back(),
B[i] can help us make the subarray length shorter and sum bigger. So no need to keep d.back() in our deque.
Q: Why keep the deque increase?
A: If B[i] <= B[d.back()] and moreover we already know that i > d.back(), it means that compared with d.back(),
B[i] can help us make the subarray length shorter and sum bigger. So no need to keep d.back() in our deque.
More detailed on this, we always add at the LAST position
B[d.back] <- B[i] <- ... <- B[future id]
B[future id] - B[d.back()] >= k && B[d.back()] >= B[i]
B[future id] - B[i] >= k too
so no need to keep B[d.back()]
*/
class Solution {
public int shortestSubarray(int[] A, int K) {
int N = A.length, res = N + 1;
int[] B = new int[N + 1];
for (int i = 0; i < N; i++) {
B[i + 1] = B[i] + A[i];
}
Deque<Integer> d = new ArrayDeque<>();
for (int i = 0; i < N + 1; i++) {
while (d.size() > 0 && B[i] - B[d.getFirst()] >= K) {
res = Math.min(res, i - d.pollFirst());
}
while (d.size() > 0 && B[i] <= B[d.getLast()]) {
d.pollLast();
}
d.addLast(i);
}
return res <= N ? res : -1;
}
}
622. Design Circular Queue
Description
Design your implementation of the circular queue. The circular queue is a linear data structure in which the operations are performed based on FIFO (First In First Out) principle and the last position is connected back to the first position to make a circle. It is also called “Ring Buffer”.
One of the benefits of the circular queue is that we can make use of the spaces in front of the queue. In a normal queue, once the queue becomes full, we cannot insert the next element even if there is a space in front of the queue. But using the circular queue, we can use the space to store new values.
Your implementation should support following operations:
MyCircularQueue(k): Constructor, set the size of the queue to be k.
Front: Get the front item from the queue. If the queue is empty, return -1.
Rear: Get the last item from the queue. If the queue is empty, return -1.
enQueue(value): Insert an element into the circular queue. Return true if the operation is successful.
deQueue(): Delete an element from the circular queue. Return true if the operation is successful.
isEmpty(): Checks whether the circular queue is empty or not.
isFull(): Checks whether the circular queue is full or not.
Example:
MyCircularQueue circularQueue = new MyCircularQueue(3); // set the size to be 3
circularQueue.enQueue(1); // return true
circularQueue.enQueue(2); // return true
circularQueue.enQueue(3); // return true
circularQueue.enQueue(4); // return false, the queue is full
circularQueue.Rear(); // return 3
circularQueue.isFull(); // return true
circularQueue.deQueue(); // return true
circularQueue.enQueue(4); // return true
circularQueue.Rear(); // return 4
Note:
All values will be in the range of [0, 1000].
The number of operations will be in the range of [1, 1000].
Please do not use the built-in Queue library.
Solution
class MyCircularQueue {
Node head;
Node tail;
int capacity;
int count;
/**
* Initialize your data structure here. Set the size of the queue to be k.
*/
public MyCircularQueue(int k) {
head = new Node(0);
tail = new Node(0);
head.next = tail;
tail.pre = head;
capacity = k;
count = 0;
}
/**
* Insert an element into the circular queue. Return true if the operation is successful.
*/
public boolean enQueue(int value) {
if (isFull()) {
return false;
}
Node last = tail.pre;
Node temp = new Node(value);
last.next = temp;
temp.pre = last;
temp.next = tail;
tail.pre = temp;
count++;
return true;
}
/**
* Delete an element from the circular queue. Return true if the operation is successful.
*/
public boolean deQueue() {
if (isEmpty()) {
return false;
}
count--;
Node temp = head.next;
Node next_temp = temp.next;
head.next = next_temp;
next_temp.pre = head;
return true;
}
/**
* Get the front item from the queue.
*/
public int Front() {
if (isEmpty()) {
return -1;
}
return head.next.val;
}
/**
* Get the last item from the queue.
*/
public int Rear() {
if (isEmpty()) {
return -1;
}
return tail.pre.val;
}
/**
* Checks whether the circular queue is empty or not.
*/
public boolean isEmpty() {
return count == 0;
}
/**
* Checks whether the circular queue is full or not.
*/
public boolean isFull() {
return capacity == count;
}
}
class Node {
Node pre;
Node next;
int val;
public Node(int val) {
this.val = val;
pre = this;
next = this;
}
}
/**
* Your MyCircularQueue object will be instantiated and called as such: MyCircularQueue obj = new MyCircularQueue(k); boolean param_1 = obj.enQueue(value);
* boolean param_2 = obj.deQueue(); int param_3 = obj.Front(); int param_4 = obj.Rear(); boolean param_5 = obj.isEmpty(); boolean param_6 = obj.isFull();
*/
2020-06-23
353. Design Snake Game
Description
Design a Snake game that is played on a device with screen size = width x height. Play the game online if you are not familiar with the game.
The snake is initially positioned at the top left corner (0,0) with length = 1 unit.
You are given a list of food’s positions in row-column order. When a snake eats the food, its length and the game’s score both increase by 1.
Each food appears one by one on the screen. For example, the second food will not appear until the first food was eaten by the snake.
When a food does appear on the screen, it is guaranteed that it will not appear on a block occupied by the snake.
Example:
Given width = 3, height = 2, and food = [[1,2],[0,1]].
Snake snake = new Snake(width, height, food);
Initially the snake appears at position (0,0) and the food at (1,2).
|S| | |
| | |F|
snake.move("R"); -> Returns 0
| |S| |
| | |F|
snake.move("D"); -> Returns 0
| | | |
| |S|F|
snake.move("R"); -> Returns 1 (Snake eats the first food and right after that, the second food appears at (0,1) )
| |F| |
| |S|S|
snake.move("U"); -> Returns 1
| |F|S|
| | |S|
snake.move("L"); -> Returns 2 (Snake eats the second food)
| |S|S|
| | |S|
snake.move("U"); -> Returns -1 (Game over because snake collides with border)
Solution
//use Integer to store position info to avoid using board[][]
class SnakeGame {
/** Initialize your data structure here.
@param width - screen width
@param height - screen height
@param food - A list of food positions
E.g food = [[1,1], [1,0]] means the first food is positioned at [1,1], the second is at [1,0].
**/
Set<Integer> set; // this copy is good for fast loop-up for eating body case
Deque<Integer> body; // this copy is good for updating tail
int score;
int[][] food;
int foodIndex;
int width;
int height;
public SnakeGame(int width, int height, int[][] food) {
this.width = width;
this.height = height;
this.food = food;
set = new HashSet<>();
set.add(0); //intially at [0][0]
body = new LinkedList<>();
body.offerLast(0);
}
/** Moves the snake.
@param direction - 'U' = Up, 'L' = Left, 'R' = Right, 'D' = Down
@return The game's score after the move. Return -1 if game over.
Game over when snake crosses the screen boundary or bites its body. */
public int move(String direction) {
if (score == -1) {
return -1;
}
int rowHead = body.peekFirst() / width;
int colHead = body.peekFirst() % width;
switch (direction) {
case "U" : rowHead--;
break;
case "D" : rowHead++;
break;
case "L" : colHead--;
break;
default : colHead++;
}
int head = rowHead * width + colHead;
set.remove(body.peekLast()); // new head is legal to be in old tail's position, remove from set temporarily
if (rowHead < 0 || rowHead == height || colHead < 0 || colHead == width || set.contains(head)) {
return score = -1;
}
// add head for case2 and case3
set.add(head);
body.offerFirst(head);
//case2: eating food, keep tail, add head
if (foodIndex < food.length && rowHead == food[foodIndex][0] && colHead == food[foodIndex][1]) {
set.add(body.peekLast()); // old tail does not change, so add it back to set
foodIndex++;
return ++score;
}
//case3: normal move, remove tail, add head
body.pollLast();
return score;
}
}
/**
* Your SnakeGame object will be instantiated and called as such:
* SnakeGame obj = new SnakeGame(width, height, food);
* int param_1 = obj.move(direction);
*/
464. Can I Win
Description
In the “100 game,” two players take turns adding, to a running total, any integer from 1..10. The player who first causes the running total to reach or exceed 100 wins.
What if we change the game so that players cannot re-use integers?
For example, two players might take turns drawing from a common pool of numbers of 1..15 without replacement until they reach a total >= 100.
Given an integer maxChoosableInteger and another integer desiredTotal, determine if the first player to move can force a win, assuming both players play optimally.
You can always assume that maxChoosableInteger will not be larger than 20 and desiredTotal will not be larger than 300.
Example
Input:
maxChoosableInteger = 10
desiredTotal = 11
Output:
false
Explanation:
No matter which integer the first player choose, the first player will lose.
The first player can choose an integer from 1 up to 10.
If the first player choose 1, the second player can only choose integers from 2 up to 10.
The second player will win by choosing 10 and get a total = 11, which is >= desiredTotal.
Same with other integers chosen by the first player, the second player will always win.
Solution
import java.util.*;
public class Solution {
Map<String, Boolean> map;
boolean[] used;
public boolean canIWin(int maxChoosableInteger, int desiredTotal) {
int sum = (1 + maxChoosableInteger) * maxChoosableInteger / 2;
if (sum < desiredTotal) {
return false;
}
if (desiredTotal <= 0) {
return true;
}
map = new HashMap();
used = new boolean[maxChoosableInteger + 1];
return helper(desiredTotal);
}
public boolean helper(int desiredTotal) {
if (desiredTotal <= 0) {
return false;
}
String key = Arrays.toString(used);
if (!map.containsKey(key)) {
// try every unchosen number as next step
for (int i = 1; i < used.length; i++) {
if (!used[i]) {
used[i] = true;
// check whether this lead to a win (i.e. the other player lose)
if (!helper(desiredTotal - i)) {
map.put(key, true);
used[i] = false;
return true;
}
used[i] = false;
}
}
map.put(key, false);
}
return map.get(key);
}
}
2020-06-24
486. Predict the Winner
Description
Given an array of scores that are non-negative integers. Player 1 picks one of the numbers from either end of the array followed by the player 2 and then player 1 and so on. Each time a player picks a number, that number will not be available for the next player. This continues until all the scores have been chosen. The player with the maximum score wins.
Given an array of scores, predict whether player 1 is the winner. You can assume each player plays to maximize his score.
Example 1:
Input: [1, 5, 2]
Output: False
Explanation: Initially, player 1 can choose between 1 and 2.
If he chooses 2 (or 1), then player 2 can choose from 1 (or 2) and 5. If player 2 chooses 5, then player 1 will be left with 1 (or 2).
So, final score of player 1 is 1 + 2 = 3, and player 2 is 5.
Hence, player 1 will never be the winner and you need to return False.
Example 2:
Input: [1, 5, 233, 7]
Output: True
Explanation: Player 1 first chooses 1. Then player 2 have to choose between 5 and 7. No matter which number player 2 choose, player 1 can choose 233.
Finally, player 1 has more score (234) than player 2 (12), so you need to return True representing player1 can win.
Note:
1 <= length of the array <= 20.
Any scores in the given array are non-negative integers and will not exceed 10,000,000.
If the scores of both players are equal, then player 1 is still the winner.
Solution
/**
dp[left][right] is the max point I can get more than opponent
**/
class Solution {
public boolean PredictTheWinner(int[] nums) {
int len = nums.length;
int[][] dp = new int[len][len];
for(int i = 0 ;i<len;i++){
dp[i][i] = nums[i];
}
return helper(nums,0,len-1,dp)>=0;
}
private int helper(int[] nums, int left, int right, int[][]dp){
if(left > right){
return 0;
}
if(dp[left][right]!=0){
return dp[left][right];
}
//max point opponent can get more than me if we pick left one.
int resRemoveLeft = helper(nums,left+1,right,dp);
int resRemoveRight = helper(nums,left, right-1,dp);
//max point I can get is the current picked number - opponent more than me.
int res = Math.max(nums[left]-resRemoveLeft,nums[right]-resRemoveRight);
dp[left][right] = res;
return res;
}
}
1266. Minimum Time Visiting All Points
Description
On a plane there are n points with integer coordinates points[i] = [xi, yi]. Your task is to find the minimum time in seconds to visit all points.
You can move according to the next rules:
In one second always you can either move vertically, horizontally by one unit or diagonally (it means to move one unit vertically and one unit horizontally in one second). You have to visit the points in the same order as they appear in the array.
Example 1:
Input: points = [[1,1],[3,4],[-1,0]]
Output: 7
Explanation: One optimal path is [1,1] -> [2,2] -> [3,3] -> [3,4] -> [2,3] -> [1,2] -> [0,1] -> [-1,0]
Time from [1,1] to [3,4] = 3 seconds
Time from [3,4] to [-1,0] = 4 seconds
Total time = 7 seconds
Example 2:
Input: points = [[3,2],[-2,2]]
Output: 5
Solution
class Solution {
public int minTimeToVisitAllPoints(int[][] points) {
int sum = 0;
for (int i = 1; i < points.length; i++) {
int diff_x = Math.abs(points[i][0] - points[i - 1][0]);
int diff_y = Math.abs(points[i][1] - points[i - 1][1]);
sum += diff_x + diff_y - Math.min(diff_x, diff_y);
}
return sum;
}
}
892. Surface Area of 3D Shapes
Description
On a N * N grid, we place some 1 * 1 * 1 cubes.
Each value v = grid[i][j] represents a tower of v cubes placed on top of grid cell (i, j).
Return the total surface area of the resulting shapes.
Example 1:
Input: [[2]]
Output: 10
Example 2:
Input: [[1,2],[3,4]]
Output: 34
Example 3:
Input: [[1,0],[0,2]]
Output: 16
Example 4:
Input: [[1,1,1],[1,0,1],[1,1,1]]
Output: 32
Example 5:
Input: [[2,2,2],[2,1,2],[2,2,2]]
Output: 46
Note:
1 <= N <= 50
0 <= grid[i][j] <= 50
Solution
//count all the diff between all towers.
class Solution {
public int surfaceArea(int[][] grid) {
int sum = 0;
int len = grid.length;
for(int i = 0;i<len;i++){
sum += grid[i][0];
sum += grid[i][len-1];
//to count top and btm.
if(grid[i][0]!=0){
sum+=2;
}
for(int j=1;j<len;j++){
//to count top and btm.
if(grid[i][j]!=0){
sum+=2;
}
//sum up all diff.
sum += Math.abs(grid[i][j]-grid[i][j-1]);
}
}
for(int j = 0;j<len;j++){
sum += grid[0][j];
sum += grid[len-1][j];
for(int i = 1;i<len;i++){
sum += Math.abs(grid[i][j]-grid[i-1][j]);
}
}
return sum;
}
}
963. Minimum Area Rectangle II
Description
Given a set of points in the xy-plane, determine the minimum area of any rectangle formed from these points, with sides not necessarily parallel to the x and y axes.
If there isn’t any rectangle, return 0.
Example 1:
Input: [[1,2],[2,1],[1,0],[0,1]]
Output: 2.00000
Explanation: The minimum area rectangle occurs at [1,2],[2,1],[1,0],[0,1], with an area of 2.
Example 2:
Input: [[0,1],[2,1],[1,1],[1,0],[2,0]]
Output: 1.00000
Explanation: The minimum area rectangle occurs at [1,0],[1,1],[2,1],[2,0], with an area of 1.
Example 3:
Input: [[0,3],[1,2],[3,1],[1,3],[2,1]]
Output: 0
Explanation: There is no possible rectangle to form from these points.
Example 4:
Input: [[3,1],[1,1],[0,1],[2,1],[3,3],[3,2],[0,2],[2,3]]
Output: 2.00000
Explanation: The minimum area rectangle occurs at [2,1],[2,3],[3,3],[3,1], with an area of 2.
Note:
1 <= points.length <= 50
0 <= points[i][0] <= 40000
0 <= points[i][1] <= 40000
All points are distinct.
Answers within 10^-5 of the actual value will be accepted as correct.
Solution
/**
Find all points pair who have the same distance and also the same center point.
pair them and find the max area rectangle
*/
class Solution {
public double minAreaFreeRect(int[][] points) {
int len = points.length;
double res = Double.MAX_VALUE;
if (len < 4) {
return 0.0;
}
Map<String, List<int[]>> map = new HashMap<>();
// int[] is the index of two points forming the diagonal
for (int i = 0; i < len; i++) {
for (int j = i + 1; j < len; j++) {
long dis = (points[i][0] - points[j][0]) * (points[i][0] - points[j][0]) + (points[i][1] - points[j][1]) * (points[i][1] - points[j][1]);
double centerX = (double) (points[j][0] + points[i][0]) / 2;
// centerX and centerY is the coordinate of the diagonal center
double centerY = (double) (points[j][1] + points[i][1]) / 2;
String key = "" + dis + "+" + centerX + "+" + centerY;
// key includes the length of the diagonal and the coordinate of the diagonal center
if (map.get(key) == null) {
map.put(key, new ArrayList<int[]>());
}
map.get(key).add(new int[]{i, j});
}
}
for (String key : map.keySet()) {
if (map.get(key).size() > 1) {
List<int[]> list = map.get(key);
for (int i = 0; i < list.size(); i++) {
// there could be multiple rectangles inside
for (int j = i + 1; j < list.size(); j++) {
int p1 = list.get(i)[0];
// p1, p2 and p3 are the three vertices of a rectangle
int p2 = list.get(j)[0];
int p3 = list.get(j)[1];
// len1 and len2 are the length of the sides of a rectangle
double len1 = Math.sqrt(
(points[p1][0] - points[p2][0]) * (points[p1][0] - points[p2][0]) + (points[p1][1] - points[p2][1]) * (points[p1][1]
- points[p2][1]));
double len2 = Math.sqrt(
(points[p1][0] - points[p3][0]) * (points[p1][0] - points[p3][0]) + (points[p1][1] - points[p3][1]) * (points[p1][1]
- points[p3][1]));
double area = len1 * len2;
res = Math.min(res, area);
}
}
}
}
return res == Double.MAX_VALUE ? 0.0 : res;
}
}
2020-06-25
1401. Circle and Rectangle Overlapping
Description
Given a circle represented as (radius, x_center, y_center) and an axis-aligned rectangle represented as (x1, y1, x2, y2), where (x1, y1) are the coordinates of the bottom-left corner, and (x2, y2) are the coordinates of the top-right corner of the rectangle.
Return True if the circle and rectangle are overlapped otherwise return False.
In other words, check if there are any point (xi, yi) such that belongs to the circle and the rectangle at the same time.
Example 1:
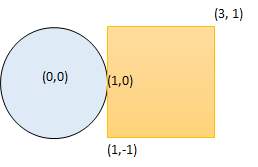
Input: radius = 1, x_center = 0, y_center = 0, x1 = 1, y1 = -1, x2 = 3, y2 = 1
Output: true
Explanation: Circle and rectangle share the point (1,0)
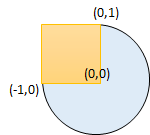
Example 2:
Input: radius = 1, x_center = 0, y_center = 0, x1 = -1, y1 = 0, x2 = 0, y2 = 1
Output: true
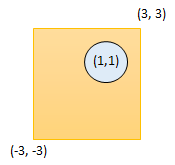
Example 3:
Input: radius = 1, x_center = 1, y_center = 1, x1 = -3, y1 = -3, x2 = 3, y2 = 3
Output: true
Example 4:
Input: radius = 1, x_center = 1, y_center = 1, x1 = 1, y1 = -3, x2 = 2, y2 = -1
Output: false
Constraints:
1 <= radius <= 2000
-10^4 <= x_center, y_center, x1, y1, x2, y2 <= 10^4
x1 < x2
y1 < y2
Solution
class Solution {
public boolean checkOverlap(int radius, int x_center, int y_center, int x1, int y1, int x2, int y2) {
// Find the closest point to the circle within the rectangle
//case 1: center, x1, x2 -> x1
//case 2: x1, center, x2 -> val
//case 3: x1, x2, center -> x2
int closestX = clamp(x_center, x1, x2);
int closestY = clamp(y_center, y1, y2);
// Calculate the distance between the circle's center and this closest point
int distanceX = x_center - closestX;
int distanceY = y_center - closestY;
// If the distance is less than the circle's radius, an intersection occurs
int distanceSquared = (distanceX * distanceX) + (distanceY * distanceY);
return distanceSquared <= (radius * radius);
}
public int clamp(int val, int min, int max) {
return Math.max(min, Math.min(max, val));
}
}
1229. Meeting Scheduler
Description
Given the availability time slots arrays slots1 and slots2 of two people and a meeting duration duration, return the earliest time slot that works for both of them and is of duration duration.
If there is no common time slot that satisfies the requirements, return an empty array.
The format of a time slot is an array of two elements [start, end] representing an inclusive time range from start to end.
It is guaranteed that no two availability slots of the same person intersect with each other. That is, for any two time slots [start1, end1] and [start2, end2] of the same person, either start1 > end2 or start2 > end1.
Example 1:
Input: slots1 = [[10,50],[60,120],[140,210]], slots2 = [[0,15],[60,70]], duration = 8
Output: [60,68]
Example 2:
Input: slots1 = [[10,50],[60,120],[140,210]], slots2 = [[0,15],[60,70]], duration = 12
Output: []
Constraints:
1 <= slots1.length, slots2.length <= 10^4
slots1[i].length, slots2[i].length == 2
slots1[i][0] < slots1[i][1]
slots2[i][0] < slots2[i][1]
0 <= slots1[i][j], slots2[i][j] <= 10^9
1 <= duration <= 10^6
Solution
import java.util.*;
class Solution {
public List<Integer> minAvailableDuration(int[][] slots1, int[][] slots2, int duration) {
Arrays.sort(slots1, (a,b)->a[0]-b[0]); // sort increasing by start time
Arrays.sort(slots2, (a,b)->a[0]-b[0]); // sort increasing by start time
int i = 0, j = 0;
int n1 = slots1.length, n2 = slots2.length;
while (i < n1 && j < n2) {
// Find intersect between slots1[i] and slots2[j]
int intersectStart = Math.max(slots1[i][0], slots2[j][0]);
int intersectEnd = Math.min(slots1[i][1], slots2[j][1]);
if (intersectStart + duration <= intersectEnd) // Found the result
return Arrays.asList(intersectStart, intersectStart + duration);
else if (slots1[i][1] < slots2[j][1])
i++;
else
j++;
}
return new ArrayList<>();
}
}
1272. Remove Interval
Description
Given a sorted list of disjoint intervals, each interval intervals[i] = [a, b] represents the set of real numbers x such that a <= x < b.
We remove the intersections between any interval in intervals and the interval toBeRemoved.
Return a sorted list of intervals after all such removals.
Example 1:
Input: intervals = [[0,2],[3,4],[5,7]], toBeRemoved = [1,6]
Output: [[0,1],[6,7]]
Example 2:
Input: intervals = [[0,5]], toBeRemoved = [2,3]
Output: [[0,2],[3,5]]
Constraints:
1 <= intervals.length <= 10^4
-10^9 <= intervals[i][0] < intervals[i][1] <= 10^9
Solution
class Solution {
public List<List<Integer>> removeInterval(int[][] intervals, int[] toBeRemoved) {
List<List<Integer>> res = new LinkedList<>();
for (int i = 0; i < intervals.length; i++) {
int[] interval = intervals[i];
if (interval[1] < toBeRemoved[0] || interval[0] > toBeRemoved[1]) {
res.add(new ArrayList<Integer>() );
} else if (interval[0] <= toBeRemoved[0] && interval[1] <= toBeRemoved[1]) {
res.add(new ArrayList<Integer>() );
} else if (interval[0] >= toBeRemoved[0] && interval[1] >= toBeRemoved[1]) {
res.add(new ArrayList<Integer>() );
} else if (interval[0] < toBeRemoved[0] && interval[1] > toBeRemoved[1]) {
res.add(new ArrayList<Integer>() );
res.add(new ArrayList<Integer>() );
}
}
return res;
}
}
2020-06-26
470. Implement Rand10() Using Rand7()
Description
Given a function rand7 which generates a uniform random integer in the range 1 to 7, write a function rand10 which generates a uniform random integer in the range 1 to 10.
Do NOT use system’s Math.random().
Example 1:
Input: 1
Output: [7]
Example 2:
Input: 2
Output: [8,4]
Example 3:
Input: 3
Output: [8,1,10]
Note:
rand7 is predefined.
Each testcase has one argument: n, the number of times that rand10 is called.
Follow up:
What is the expected value for the number of calls to rand7() function?
Could you minimize the number of calls to rand7()?
Solution
/**
rand7() -> [1,7]
7*(rand7()-1) -> [0,42]
7*(rand7()-1) + rand7() -1 -> [0,48]
so number in [0,39] are all evenly distributed.
use number in [0,39] to
*/
/**
* The rand7() API is already defined in the parent class SolBase.
* public int rand7();
* @return a random integer in the range 1 to 7
*/
class Solution extends SolBase {
public int rand10() {
int rand40 = 40;
while(rand40>=40){
rand40 = 7*(rand7() - 1)+rand7()-1;
}
return rand40 % 10 +1;
}
}
Implement randM() using randN() when M > N:
Step 1: Use randN() to generate randX(), where X >= M. In this problem, I use 7 * (rand7() - 1) + (rand7() - 1) to generate rand49() - 1.
Step 2: Use randX() to generate randM(). In this problem, I use rand49() to generate rand40() then generate rand10.
Note: N^b * (randN() - 1) + N^(b - 1) * (randN() - 1) + N^(b - 2) * (randN() - 1) + … + N^0 * (randN() - 1) generates randX() - 1, where X = N^(b + 1).
More Examples
(1) Implement rand11() using rand3():
public int rand11() {
int result = 22;
while (result >= 22) {result = 3 * 3 * (rand3() - 1) + 3 * (rand3() - 1) + (rand3() - 1);}
return result % 11 + 1;
}
Idea: rand3() -> rand27() -> rand22 -> rand11
Time Comlexity: O(27/22)
(2) Implement rand9() using rand7():
public int rand9() {
int result = 45;
while (result >= 45) {result = 7 * (rand7() - 1) + (rand7() - 1);}
return result % 9 + 1;
}
Idea: rand7() -> rand49() -> rand45() -> rand9()
Time Comlexity: O(49/45)
(3) Implement rand13() using rand6():
public int rand13() {
int result = 26;
while (result >= 26) {result = 6 * (rand6() - 1) + (rand6() - 1);}
return result % 13 + 1;
}
Idea: rand6() -> rand36() -> rand26 -> rand13()
Time Comlexity: O(36/26)
478. Generate Random Point in a Circle
Description
Given the radius and x-y positions of the center of a circle, write a function randPoint which generates a uniform random point in the circle.
Note:
input and output values are in floating-point. radius and x-y position of the center of the circle is passed into the class constructor. a point on the circumference of the circle is considered to be in the circle. randPoint returns a size 2 array containing x-position and y-position of the random point, in that order.
Example 1:
Input:
["Solution","randPoint","randPoint","randPoint"]
[[1,0,0],[],[],[]]
Output: [null,[-0.72939,-0.65505],[-0.78502,-0.28626],[-0.83119,-0.19803]]
Example 2:
Input:
["Solution","randPoint","randPoint","randPoint"]
[[10,5,-7.5],[],[],[]]
Output: [null,[11.52438,-8.33273],[2.46992,-16.21705],[11.13430,-12.42337]]
Explanation of Input Syntax:
The input is two lists: the subroutines called and their arguments. Solution's constructor has three arguments, the radius, x-position of the center, and y-position of the center of the circle. randPoint has no arguments. Arguments are always wrapped with a list, even if there aren't any.
Solution
class Solution {
double radius, x_center, y_center;
public Solution(double radius, double x_center, double y_center) {
this.radius = radius;
this.x_center = x_center;
this.y_center = y_center;
}
public double[] randPoint() {
/**
* let A be the area of the circle.
* A = pi*r^2
* dA = pi * d(r^2)
* therefore A is linear with r^2
*/
double len = Math.sqrt(Math.random()) * radius;
double deg = Math.random() * 2 * Math.PI;
double x = x_center + len * Math.cos(deg);
double y = y_center + len * Math.sin(deg);
return new double[]{x, y};
}
}
497. Random Point in Non-overlapping Rectangles
Description
Given a list of non-overlapping axis-aligned rectangles rects, write a function pick which randomly and uniformily picks an integer point in the space covered by the rectangles.
Note:
An integer point is a point that has integer coordinates. A point on the perimeter of a rectangle is included in the space covered by the rectangles. ith rectangle = rects[i] = [x1,y1,x2,y2], where [x1, y1] are the integer coordinates of the bottom-left corner, and [x2, y2] are the integer coordinates of the top-right corner. length and width of each rectangle does not exceed 2000. 1 <= rects.length <= 100 pick return a point as an array of integer coordinates [p_x, p_y] pick is called at most 10000 times.
Example 1:
Input:
["Solution","pick","pick","pick"]
[[[[1,1,5,5]]],[],[],[]]
Output:
[null,[4,1],[4,1],[3,3]]
Example 2:
Input:
["Solution","pick","pick","pick","pick","pick"]
[[[[-2,-2,-1,-1],[1,0,3,0]]],[],[],[],[],[]]
Output:
[null,[-1,-2],[2,0],[-2,-1],[3,0],[-2,-2]]
Explanation of Input Syntax:
The input is two lists: the subroutines called and their arguments. Solution's constructor has one argument, the array of rectangles rects. pick has no arguments. Arguments are always wrapped with a list, even if there aren't any.
Solution
class Solution {
TreeMap<Integer, Integer> map;
int[][] arrays;
int sum;
Random rnd= new Random();
public Solution(int[][] rects) {
arrays = rects;
map = new TreeMap<>();
sum = 0;
for(int i = 0; i < rects.length; i++) {
int[] rect = rects[i];
// the right part means the number of points can be picked in this rectangle
//right column can also be considered, so [0,1] have 0 and 1 posiibility.
sum += (rect[2] - rect[0] + 1) * (rect[3] - rect[1] + 1);
map.put(sum, i);
}
}
public int[] pick() {
// nextInt(sum) returns a num in [0, sum -1]. After added by 1, it becomes [1, sum]
int c = map.ceilingKey( rnd.nextInt(sum) + 1);
return pickInRect(arrays[map.get(c)]);
}
private int[] pickInRect(int[] rect) {
int left = rect[0], right = rect[2], bot = rect[1], top = rect[3];
return new int[]{left + rnd.nextInt(right - left + 1), bot + rnd.nextInt(top - bot + 1) };
}
}
329. Longest Increasing Path in a Matrix
Description
Given an integer matrix, find the length of the longest increasing path.
From each cell, you can either move to four directions: left, right, up or down. You may NOT move diagonally or move outside of the boundary (i.e. wrap-around is not allowed).
Example 1:
Input: nums =
[
[9,9,4],
[6,6,8],
[2,1,1]
]
Output: 4
Explanation: The longest increasing path is [1, 2, 6, 9].
Example 2:
Input: nums =
[
[3,4,5],
[3,2,6],
[2,2,1]
]
Output: 4
Explanation: The longest increasing path is [3, 4, 5, 6]. Moving diagonally is not allowed.
Solution
class Solution {
public static final int[][] dirs = [[0, 1], [1, 0], [0, -1], [-1, 0]];
public int longestIncreasingPath(int[][] matrix) {
if (matrix.length == 0) {
return 0;
}
int m = matrix.length, n = matrix[0].length;
int[][] cache = new int[m][n];
int max = 1;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
int len = dfs(matrix, i, j, m, n, cache);
max = Math.max(max, len);
}
}
return max;
}
public int dfs(int[][] matrix, int i, int j, int m, int n, int[][] cache) {
if (cache[i][j] != 0) {
return cache[i][j];
}
int max = 1;
for (int[] dir : dirs) {
int x = i + dir[0], y = j + dir[1];
if (x < 0 || x >= m || y < 0 || y >= n || matrix[x][y] <= matrix[i][j]) {
continue;
}
int len = 1 + dfs(matrix, x, y, m, n, cache);
max = Math.max(max, len);
}
cache[i][j] = max;
return max;
}
}
Topological sort
class Solution {
public int longestIncreasingPath(int[][] matrix) {
if (matrix.length == 0 || matrix[0].length == 0) {
return 0;
}
int row = matrix.length;
int col = matrix[0].length;
int[][] dirs = new int[][][[0, 1], [1, 0], [0, -1], [-1, 0]];
HashMap<Integer, HashSet<Integer>> graph = new HashMap<>();
HashMap<Integer, Integer> degree = new HashMap<>();
HashMap<Integer, Integer> step = new HashMap<>();
for (int i = 0; i < row; i++) {
for (int j = 0; j < col; j++) {
int idx = i * col + j;
graph.putIfAbsent(idx, new HashSet<>());
degree.putIfAbsent(idx, 0);
for (int[] dir : dirs) {
int next_i = i + dir[0];
int next_j = j + dir[1];
if (next_i >= 0 && next_i < row && next_j >= 0 && next_j < col && matrix[i][j] < matrix[next_i][next_j]) {
int next_idx = next_i * col + next_j;
graph.get(idx).add(next_idx);
degree.put(next_idx, degree.getOrDefault(next_idx, 0) + 1);
}
}
}
}
Queue<Integer> queue = new LinkedList<>();
for (int node : degree.keySet()) {
if (degree.get(node) == 0) {
queue.add(node);
}
}
int countMax = 1;
while (!queue.isEmpty()) {
int idx = queue.poll();
int i = idx / col;
int j = idx % col;
step.putIfAbsent(idx, 1);
for (int child : graph.get(idx)) {
int next_i = child / col;
int next_j = child % col;
int degree_child = degree.get(child);
degree.put(child, degree_child - 1);
if (degree_child == 1) {
queue.offer(child);
step.put(child, Math.max(step.getOrDefault(child, 1), step.get(idx) + 1));
countMax = Math.max(countMax, step.get(child));
}
}
}
return countMax;
}
}
444. Sequence Reconstruction
Description
Check whether the original sequence org can be uniquely reconstructed from the sequences in seqs. The org sequence is a permutation of the integers from 1 to n, with 1 ≤ n ≤ 104. Reconstruction means building a shortest common supersequence of the sequences in seqs (i.e., a shortest sequence so that all sequences in seqs are subsequences of it). Determine whether there is only one sequence that can be reconstructed from seqs and it is the org sequence.
Example 1:
Input: org = [1,2,3], seqs = [[1,2],[1,3]]
Output: false
Explanation: [1,2,3] is not the only one sequence that can be reconstructed, because [1,3,2] is also a valid sequence that can be reconstructed.
Example 2:
Input: org = [1,2,3], seqs = [[1,2]]
Output: false
Explanation: The reconstructed sequence can only be [1,2].
Example 3:
Input: org = [1,2,3], seqs = [[1,2],[1,3],[2,3]]
Output: true
Explanation: The sequences [1,2], [1,3], and [2,3] can uniquely reconstruct the original sequence [1,2,3].
Example 4:
Input: org = [4,1,5,2,6,3], seqs = [[5,2,6,3],[4,1,5,2]]
Output: true
Constraints:
1 <= n <= 10^4
org is a permutation of {1,2,...,n}.
seqs[i][j] fits in a 32-bit signed integer.
Solution
public class Solution {
public boolean sequenceReconstruction(int[] org, int[][] seqs) {
Map<Integer, Set<Integer>> map = new HashMap<>();
Map<Integer, Integer> indegree = new HashMap<>();
//Build graph and degree.
for (int[] seq : seqs) {
if (seq.length == 1) {
if (!map.containsKey(seq[0])) {
map.put(seq[0], new HashSet<>());
indegree.put(seq[0], 0);
}
} else {
for (int i = 0; i < seq.length - 1; i++) {
if (!map.containsKey(seq[i])) {
map.put(seq[i], new HashSet<>());
indegree.put(seq[i], 0);
}
if (!map.containsKey(seq[i + 1])) {
map.put(seq[i + 1], new HashSet<>());
indegree.put(seq[i + 1], 0);
}
if (map.get(seq[i]).add(seq[i + 1])) {
indegree.put(seq[i + 1], indegree.get(seq[i + 1]) + 1);
}
}
}
}
Queue<Integer> queue = new LinkedList<>();
for (Map.Entry<Integer, Integer> entry : indegree.entrySet()) {
if (entry.getValue() == 0) {
queue.offer(entry.getKey());
}
}
int index = 0;
while (!queue.isEmpty()) {
int size = queue.size();
//only one element should be allowed in the queue
//otherwise you can have multiple choices.
if (size > 1) {
return false;
}
int curr = queue.poll();
index++;
//should not reach the end of org or the current one is not equal to what it supposed to be in the org
if (index >= org.length || curr != org[index]) {
return false;
}
for (int next : map.get(curr)) {
indegree.put(next, indegree.get(next) - 1);
if (indegree.get(next) == 0) {
queue.offer(next);
}
}
}
//should reached the end and no element left.
return index == org.length && index == map.size();
}
}
2020-06-27
403. Frog Jump
Description
A frog is crossing a river. The river is divided into x units and at each unit there may or may not exist a stone. The frog can jump on a stone, but it must not jump into the water.
Given a list of stones’ positions (in units) in sorted ascending order, determine if the frog is able to cross the river by landing on the last stone. Initially, the frog is on the first stone and assume the first jump must be 1 unit.
If the frog’s last jump was k units, then its next jump must be either k - 1, k, or k + 1 units. Note that the frog can only jump in the forward direction.
Note:
The number of stones is ≥ 2 and is < 1,100. Each stone’s position will be a non-negative integer < 231. The first stone’s position is always 0.
Example 1:
[0,1,3,5,6,8,12,17]
There are a total of 8 stones.
The first stone at the 0th unit, second stone at the 1st unit,
third stone at the 3rd unit, and so on...
The last stone at the 17th unit.
Return true. The frog can jump to the last stone by jumping
1 unit to the 2nd stone, then 2 units to the 3rd stone, then
2 units to the 4th stone, then 3 units to the 6th stone,
4 units to the 7th stone, and 5 units to the 8th stone.
Example 2:
[0,1,2,3,4,8,9,11]
Return false. There is no way to jump to the last stone as
the gap between the 5th and 6th stone is too large.
Solution
class Solution {
public boolean canCross(int[] stones) {
if (stones.length == 0) {
return false;
}
int end = stones[stones.length-1];
HashMap<Integer, HashSet<Integer>> map = new HashMap<>();
map.put(0, new HashSet<>());
map.get(0).add(1);
for (int stone : stones) {
for (int step : map.getOrDefault(stone, new HashSet<Integer>())) {
int reach = stone + step;
if(reach == end){
return true;
}
if(!map.containsKey(reach)){
map.put(reach,new HashSet<Integer>());
}
HashSet<Integer> reachSet = map.get(reach);
reachSet.add(step);
reachSet.add(step+1);
if(step-1>0){
reachSet.add(step-1);
}
}
}
return false;
}
}
DP solution
+----+ +----+ +----+ +----+
stone: | S1 | | S2 | | S3 | | S4 |
____|____|____|____|________|____|_____|____|____________
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
position:" 0 1 3 5 "
jump size: 1 [0, 1, 2] [1, 2, 3]
// Suppose we want to know if the frog can reach stone 2 (S2),
// and we know the frog must come from S1,
// dist(S1->S2) = 1 - 0 = 1, and we already know the frog is able to make a jump of size 1 at S1.
// Hence, the frog is able to reach S2, and the next jump would be 0, 1 or 2 units.
// Then, we want to know if the frog can reach stone 3 (S3),
// we know the frog must be at either S1 or S2 before reaching S3,
// If the frog comes from S1, then
// we know dist(S1->S3) = 3 - 0 = 3, and we know frog couldn't make a jump of size 3 at S1.
// So it is not possible the frog can jump from S1 to S3.
// If the frog comes from S2, then
// we know dist(S2->S3) = 3 - 1 = 2, and we know frog could make a jump of size 2 at S2.
// Hence, the frog is able to reach S3, and the next jump would be 1, 2 or 3 units.
// If we repeat doing this for the rest stones, we'll end with something like below:
Exapme 1:
index: 0 1 2 3 4 5 6 7
+---+---+---+---+---+---+---+---+
stone pos: | 0 | 1 | 3 | 5 | 6 | 8 | 12| 17|
+---+---+---+---+---+---+---+---+
k: | 1 | 0 | 1 | 1 | 0 | 1 | 3 | 5 |
| | 1 | 2 | 2 | 1 | 2 | 4 | 6 |
| | 2 | 3 | 3 | 2 | 3 | 5 | 7 |
| | | | | 3 | 4 | | |
| | | | | 4 | | | |
| | | | | | | | |
// Sub-problem and state:
let dp(i) denote a set containing all next jump size at stone i
// Recurrence relation:
for any j < i,
dist = stones[i] - stones[j];
if dist is in dp(j):
put dist - 1, dist, dist + 1 into dp(i).
// Now lets make this approach more efficient.
// BECAUSE
// 1. The number of stones is ≥ 2 and is < 1,100.
// 2. The frog is on the first stone and assume the first jump must be 1 unit.
// 3. If the frog's last jump was k units, then its next jump must be either k - 1, k, or k + 1 units,
// The maximum jump size the frog can make at each stone if possible is shown as followings:
// stone: 0, 1, 2, 3, 4, 5
// jump size: 1, 2, 3, 4, 5, 6 (suppose frog made jump with size k + 1 at each stone)
// So instead of creating a HashSet for lookup for each stone,
// we can create a boolean array with size of N + 1 (N is the number of stones),
// Like in the given example, at stone 2 the next jump could be 1, 2, 3,
// we can use a bool array to represent this like
// index: 0 1 2 3 4 5 6 7 ...
// [0, 1, 1, 1, 0, 0, 0, 0, ...]
// index is jump size, boolean value represents if the frog can make this jump.
// Then, the 2D array will be something like below.
index: 0 1 2 3 4 5 6 7
+---+---+---+---+---+---+---+---+
stone pos: | 0 | 1 | 3 | 5 | 6 | 8 | 12| 17|
+---+---+---+---+---+---+---+---+
k: 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
2 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 |
3 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 |
4 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
5 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
// Sub-problem and state:
let dp[i][j] denote at stone i, the frog can or cannot make jump of size j
// Recurrence relation:
for any j < i,
dist = stones[i] - stones[j];
if dp[j][dist]:
dp[i][dist - 1] = ture
dp[i][dist] = ture
dp[i][dist + 1] = ture
class Solution {
public boolean canCross(int[] stones) {
int N = stones.length;
boolean[][] dp = new boolean[N][N + 1];
dp[0][1] = true;
for(int i = 1; i < N; ++i){
for(int j = 0; j < i; ++j){
int diff = stones[i] - stones[j];
//can only increment one jump at a time.
//The maximum jump size the frog can make at each stone is at most N+1
if(diff < 0 || diff > N || !dp[j][diff]) continue;
dp[i][diff] = true;
if(diff - 1 >= 0) dp[i][diff - 1] = true;
if(diff + 1 <= N) dp[i][diff + 1] = true;
if(i == N - 1) return true;
}
}
return false;
}
}
1152. Analyze User Website Visit Pattern
Description
We are given some website visits: the user with name username[i] visited the website website[i] at time timestamp[i].
A 3-sequence is a list of websites of length 3 sorted in ascending order by the time of their visits. (The websites in a 3-sequence are not necessarily distinct.)
Find the 3-sequence visited by the largest number of users. If there is more than one solution, return the lexicographically smallest such 3-sequence.
Example 1:
Input: username = ["joe","joe","joe","james","james","james","james","mary","mary","mary"], timestamp = [1,2,3,4,5,6,7,8,9,10], website = ["home","about","career","home","cart","maps","home","home","about","career"]
Output: ["home","about","career"]
Explanation:
The tuples in this example are:
["joe", 1, "home"]
["joe", 2, "about"]
["joe", 3, "career"]
["james", 4, "home"]
["james", 5, "cart"]
["james", 6, "maps"]
["james", 7, "home"]
["mary", 8, "home"]
["mary", 9, "about"]
["mary", 10, "career"]
The 3-sequence ("home", "about", "career") was visited at least once by 2 users.
The 3-sequence ("home", "cart", "maps") was visited at least once by 1 user.
The 3-sequence ("home", "cart", "home") was visited at least once by 1 user.
The 3-sequence ("home", "maps", "home") was visited at least once by 1 user.
The 3-sequence ("cart", "maps", "home") was visited at least once by 1 user.
Note:
3 <= N = username.length = timestamp.length = website.length <= 50
1 <= username[i].length <= 10
0 <= timestamp[i] <= 10^9
1 <= website[i].length <= 10
Both username[i] and website[i] contain only lowercase characters.
It is guaranteed that there is at least one user who visited at least 3 websites.
No user visits two websites at the same time.
Solution
class Pair {
int time;
String web;
public Pair(int time, String web) {
this.time = time;
this.web = web;
}
}
class Solution {
public List<String> mostVisitedPattern(String[] username, int[] timestamp, String[] website) {
Map<String, List<Pair>> map = new HashMap<>();
int n = username.length;
// collect the website info for every user, key: username, value: (timestamp, website)
for (int i = 0; i < n; i++) {
map.putIfAbsent(username[i], new ArrayList<>());
map.get(username[i]).add(new Pair(timestamp[i], website[i]));
}
// count map to record every 3 combination occuring time for the different user.
Map<String, Integer> count = new HashMap<>();
String res = "";
for (String key : map.keySet()) {
Set<String> set = new HashSet<>();
// this set is to avoid visit the same 3-seq in one user
List<Pair> list = map.get(key);
Collections.sort(list, (a, b) -> (a.time - b.time)); // sort by time
// brutal force O(N ^ 3)
for (int i = 0; i < list.size(); i++) {
for (int j = i + 1; j < list.size(); j++) {
for (int k = j + 1; k < list.size(); k++) {
String str = list.get(i).web + " " + list.get(j).web + " " + list.get(k).web;
if (!set.contains(str)) {
count.put(str, count.getOrDefault(str, 0) + 1);
set.add(str);
}
if (res.equals("") || count.get(res) < count.get(str) || (count.get(res) == count.get(str) && res.compareTo(str) > 0)) {
// make sure the right lexi order
res = str;
}
}
}
}
}
// grab the right answer
String[] r = res.split(" ");
List<String> result = new ArrayList<>();
for (String str : r) {
result.add(str);
}
return result;
}
}
465. Optimal Account Balancing
Description
A group of friends went on holiday and sometimes lent each other money. For example, Alice paid for Bill’s lunch for $10. Then later Chris gave Alice $5 for a taxi ride. We can model each transaction as a tuple (x, y, z) which means person x gave person y $z. Assuming Alice, Bill, and Chris are person 0, 1, and 2 respectively (0, 1, 2 are the person’s ID), the transactions can be represented as [[0, 1, 10], [2, 0, 5]].
Given a list of transactions between a group of people, return the minimum number of transactions required to settle the debt.
Note:
A transaction will be given as a tuple (x, y, z). Note that x ≠ y and z > 0.
Person's IDs may not be linear, e.g. we could have the persons 0, 1, 2 or we could also have the persons 0, 2, 6.
Example 1:
Input:
[[0,1,10], [2,0,5]]
Output:
2
Explanation:
Person #0 gave person #1 $10.
Person #2 gave person #0 $5.
Two transactions are needed. One way to settle the debt is person #1 pays person #0 and #2 $5 each.
Example 2:
Input:
[[0,1,10], [1,0,1], [1,2,5], [2,0,5]]
Output:
1
Explanation:
Person #0 gave person #1 $10.
Person #1 gave person #0 $1.
Person #1 gave person #2 $5.
Person #2 gave person #0 $5.
Therefore, person #1 only need to give person #0 $4, and all debt is settled.
Solution
import java.util.*;
class Solution {
public int minTransfers(int[][] transactions) {
HashMap<Integer, Integer> m = new HashMap<>();
for (int[] t : transactions) {
m.put(t[0], m.getOrDefault(t[0], 0) - t[2]);
m.put(t[1], m.getOrDefault(t[1], 0) + t[2]);
}
//only use values, so a list of debit
return settle(0, new ArrayList<>(m.values()));
}
int settle(int start, List<Integer> debt) {
//ignore all the 0 debit person.
while (start < debt.size() && debt.get(start) == 0) {
start++;
}
//reached the end
if (start == debt.size()) {
return 0;
}
int r = Integer.MAX_VALUE;
for (int i = start + 1; i < debt.size(); i++) {
//only if one person is debit and other is borrowing can they settle up.
if (debt.get(start) * debt.get(i) < 0) {
//temply settle it.
debt.set(i, debt.get(i) + debt.get(start));
//find all possible ways to settle.
//need to searching from start+1 but not i!
r = Math.min(r, 1 + settle(start + 1, debt));
//revert it back for next loop use.
debt.set(i, debt.get(i) - debt.get(start));
}
}
return r;
}
}
2020-06-28
950. Reveal Cards In Increasing Order
Description
In a deck of cards, every card has a unique integer. You can order the deck in any order you want.
Initially, all the cards start face down (unrevealed) in one deck.
Now, you do the following steps repeatedly, until all cards are revealed:
Take the top card of the deck, reveal it, and take it out of the deck. If there are still cards in the deck, put the next top card of the deck at the bottom of the deck. If there are still unrevealed cards, go back to step 1. Otherwise, stop. Return an ordering of the deck that would reveal the cards in increasing order.
The first entry in the answer is considered to be the top of the deck.
Example 1:
Input: [17,13,11,2,3,5,7]
Output: [2,13,3,11,5,17,7]
Explanation:
We get the deck in the order [17,13,11,2,3,5,7] (this order doesn't matter), and reorder it.
After reordering, the deck starts as [2,13,3,11,5,17,7], where 2 is the top of the deck.
We reveal 2, and move 13 to the bottom. The deck is now [3,11,5,17,7,13].
We reveal 3, and move 11 to the bottom. The deck is now [5,17,7,13,11].
We reveal 5, and move 17 to the bottom. The deck is now [7,13,11,17].
We reveal 7, and move 13 to the bottom. The deck is now [11,17,13].
We reveal 11, and move 17 to the bottom. The deck is now [13,17].
We reveal 13, and move 17 to the bottom. The deck is now [17].
We reveal 17.
Since all the cards revealed are in increasing order, the answer is correct.
Note:
1 <= A.length <= 1000
1 <= A[i] <= 10^6
A[i] != A[j] for all i != j
Solution
/**
Simply reverse the process from a sorted list.
*/
class Solution {
public int[] deckRevealedIncreasing(int[] deck) {
if (deck == null || deck.length == 0) {
return new int[]{};
}
int len = deck.length;
Deque<Integer> deque = new LinkedList<>();
Arrays.sort(deck);
deque.offerFirst(deck[len - 1]);
for (int i = len - 2; i >= 0; i--) {
int temp = deque.pollLast();
deque.addFirst(temp);
deque.addFirst(deck[i]);
}
int[] ret = new int[len];
for(int i = 0;i<len;i++){
ret[i] = deque.pollFirst();
}
return ret;
}
}
268. Missing Number
Description
Given an array containing n distinct numbers taken from 0, 1, 2, …, n, find the one that is missing from the array.
Example 1:
Input: [3,0,1]
Output: 2
Example 2:
Input: [9,6,4,2,3,5,7,0,1]
Output: 8
Solution
/**
use nums as slot, ignore number n.
*/
class Solution {
public int missingNumber(int[] nums) {
int n = nums.length;
int N = nums.length+1;
for(int i = 0;i<n;i++){
int orig = nums[i] % N;
if(orig<n){
nums[orig] += N;
}
}
for(int i = 0;i<n;i++){
if(nums[i]/N==0){
return i;
}
}
//if all number exist, it must be the last number.
return n;
}
}
717. 1-bit and 2-bit Characters
Description
We have two special characters. The first character can be represented by one bit 0. The second character can be represented by two bits (10 or 11).
Now given a string represented by several bits. Return whether the last character must be a one-bit character or not. The given string will always end with a zero.
Example 1:
Input:
bits = [1, 0, 0]
Output: True
Explanation:
The only way to decode it is two-bit character and one-bit character. So the last character is one-bit character.
Example 2:
Input:
bits = [1, 1, 1, 0]
Output: False
Explanation:
The only way to decode it is two-bit character and two-bit character. So the last character is NOT one-bit character.
Note:
1 <= len(bits) <= 1000.
bits[i] is always 0 or 1.
Solution
class Solution {
public boolean isOneBitCharacter(int[] bits) {
int n = bits.length, i = 0;
while (i < n - 1) {
if (bits[i] == 0) i++;
else i += 2;
}
return i == n - 1;
}
}
73. Set Matrix Zeroes
Description
Given a m x n matrix, if an element is 0, set its entire row and column to 0. Do it in-place.
Example 1:
Input:
[
[1,1,1],
[1,0,1],
[1,1,1]
]
Output:
[
[1,0,1],
[0,0,0],
[1,0,1]
]
Example 2:
Input:
[
[0,1,2,0],
[3,4,5,2],
[1,3,1,5]
]
Output:
[
[0,0,0,0],
[0,4,5,0],
[0,3,1,0]
]
Solution
/**
Use first col and first row to store the 0 information
meanwhile use two variables to store 0 information about first row and col.
*/
class Solution {
public void setZeroes(int[][] matrix) {
boolean firstRowZero = false, firstColZero = false;
int row = matrix.length, col = matrix[0].length;
for(int i=0;i<row;i++){
if(matrix[i][0]==0){
firstColZero=true;
break;
}
}
for(int i=0;i<col;i++){
if(matrix[0][i]==0){
firstRowZero=true;
break;
}
}
for(int i = 1;i<row;i++){
for(int j = 1;j<col;j++){
if(matrix[i][j] == 0){
matrix[i][0] = 0;
matrix[0][j] = 0;
}
}
}
for(int i=1;i<row;i++){
if(matrix[i][0]==0){
for(int j = 1;j<col;j++){
matrix[i][j] = 0;
}
}
}
for(int j=1;j<col;j++){
if(matrix[0][j]==0){
for(int i=1;i<row;i++){
matrix[i][j] = 0;
}
}
}
if(firstColZero){
for(int i = 0;i<row;i++){
matrix[i][0] = 0;
}
}
if(firstRowZero){
for(int j = 0;j<col;j++){
matrix[0][j] = 0;
}
}
}
}
832. Flipping an Image
Description
Given a binary matrix A, we want to flip the image horizontally, then invert it, and return the resulting image.
To flip an image horizontally means that each row of the image is reversed. For example, flipping [1, 1, 0] horizontally results in [0, 1, 1].
To invert an image means that each 0 is replaced by 1, and each 1 is replaced by 0. For example, inverting [0, 1, 1] results in [1, 0, 0].
Example 1:
Input: [[1,1,0],[1,0,1],[0,0,0]]
Output: [[1,0,0],[0,1,0],[1,1,1]]
Explanation: First reverse each row: [[0,1,1],[1,0,1],[0,0,0]].
Then, invert the image: [[1,0,0],[0,1,0],[1,1,1]]
Example 2:
Input: [[1,1,0,0],[1,0,0,1],[0,1,1,1],[1,0,1,0]]
Output: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]
Explanation: First reverse each row: [[0,0,1,1],[1,0,0,1],[1,1,1,0],[0,1,0,1]].
Then invert the image: [[1,1,0,0],[0,1,1,0],[0,0,0,1],[1,0,1,0]]
Notes:
1 <= A.length = A[0].length <= 20
0 <= A[i][j] <= 1
Solution
/**
If two item are diff, no need to do anything cause
after swap and toggle, it will be exactly the same
01 -> swap -> 10 -> toggle -> 01
*/
class Solution {
public int[][] flipAndInvertImage(int[][] A) {
int n = A.length;
for (int[] row : A) {
for (int i = 0; i * 2 < n; i++) {
if (row[i] == row[n - i - 1]) {
row[i] ^= 1;
row[n - i - 1] =row[i] ;
}
}
}
return A;
}
}
410. Split Array Largest Sum
Description
Given an array which consists of non-negative integers and an integer m, you can split the array into m non-empty continuous subarrays. Write an algorithm to minimize the largest sum among these m subarrays.
Note:
If n is the length of array, assume the following constraints are satisfied:
1 ≤ n ≤ 1000
1 ≤ m ≤ min(50, n)
Examples:
Input:
nums = [7,2,5,10,8]
m = 2
Output:
18
Explanation:
There are four ways to split nums into two subarrays.
The best way is to split it into [7,2,5] and [10,8],
where the largest sum among the two subarrays is only 18.
Solution
/**
1. The answer is between maximum value of input array numbers and sum of those numbers.
2. Use binary search to approach the correct answer. We have l = max number of array; r = sum of all numbers in the array;Every time we do mid = (l + r) / 2;
3. Use greedy to narrow down left and right boundaries in binary search.
3.1 Cut the array from left.
3.2 Try our best to make sure that the sum of numbers between each two cuts (inclusive) is large enough but still less than mid.
3.3 We'll end up with two results: either we can divide the array into more than m subarrays or we cannot.
If we can, it means that the mid value we pick is too small because we've already tried our best to make sure each part holds as many non-negative numbers as we can but we still have numbers left. So, it is impossible to cut the array into m parts and make sure each parts is no larger than mid. We should increase m. This leads to l = mid + 1;
If we can't, it is either we successfully divide the array into m parts and the sum of each part is less than mid, or we used up all numbers before we reach m. Both of them mean that we should lower mid because we need to find the minimum one. This leads to r = mid - 1;
*/
class Solution {
public int splitArray(int[] nums, int m) {
int max = 0;
long sum = 0;
for (int num : nums) {
max = Math.max(max, num);
sum += num;
}
if (m == 1) {
return (int) sum;
}
long l = max;
long r = sum;
while (l <= r) {
long mid = l + (r - l) / 2;
if (isValid(nums, mid, m)) {
r = mid - 1;
} else {
l = mid + 1;
}
}
return (int) l;
}
private boolean isValid(int[] nums, long target, int m) {
int count = 1;
long total = 0;
for (int num : nums) {
total += num;
if (total > target) {
total = num;
count++;
if (count > m) {
return false;
}
}
}
return true;
}
}
2020-06-29
87. Scramble String
Description
Given a string s1, we may represent it as a binary tree by partitioning it to two non-empty substrings recursively.
Below is one possible representation of s1 = "great":
great
/ \
gr eat
/ \ / \
g r e at
/ \
a t
To scramble the string, we may choose any non-leaf node and swap its two children.
For example, if we choose the node "gr" and swap its two children, it produces a scrambled string "rgeat".
rgeat
/ \
rg eat
/ \ / \
r g e at
/ \
a t
We say that "rgeat" is a scrambled string of "great".
Similarly, if we continue to swap the children of nodes "eat" and "at", it produces a scrambled string "rgtae".
rgtae
/ \
rg tae
/ \ / \
r g ta e
/ \
t a
We say that "rgtae" is a scrambled string of "great".
Given two strings s1 and s2 of the same length, determine if s2 is a scrambled string of s1.
Example 1:
Input: s1 = "great", s2 = "rgeat"
Output: true
Example 2:
Input: s1 = "abcde", s2 = "caebd"
Output: false
Solution
/**
two ways to split, check recursivly.
*/
class Solution {
Map<String, Boolean> dp = new HashMap<>();
public boolean isScramble(String s1, String s2) {
int len1 = s1.length();
int len2 = s2.length();
if (len1 != len2 || !isSameContent(s1, s2)) {
return false;
}
if (s1.equals(s2)) {
return true;
}
if (len1 == 1) {
return true;
}
String reducedS1 = reduce(s1);
String reducedS2 = reduce(s2);
String flag = reducedS1 + " " + reducedS2;
if (dp.containsKey(flag)) {
return dp.get(flag);
}
boolean res = false;
for (int i = 1; i <= len1 - 1; i++) {
String s1Left = s1.substring(0, i);
String s1Right = s1.substring(i);
//split the same way as s1, no swap.
String s2Left = s2.substring(0, i);
String s2Right = s2.substring(i);
res |= (isScramble(s1Left, s2Left) && isScramble(s1Right, s2Right));
//swap and check
s2Left = s2.substring(0, len2 - i);
s2Right = s2.substring(len2 - i);
res |= (isScramble(s1Left, s2Right) && isScramble(s1Right, s2Left));
if (res) {
break;
}
}
dp.put(flag, res);
return res;
}
public String reduce(String str) {
char[] chArr = str.toCharArray();
//Arrays.sort(chArr);
int minChar = 'z';
for (int i = 0; i < chArr.length; i++) {
minChar = Math.min(minChar, chArr[i]);
}
int offset = minChar - 'a';
for (int i = 0; i < chArr.length; i++) {
chArr[i] -= offset;
}
return String.valueOf(chArr);
}
public boolean isSameContent(String s1, String s2) {
int[] letters = new int[26];
for (int i = 0; i < s1.length(); i++) {
letters[s1.charAt(i) - 'a']++;
letters[s2.charAt(i) - 'a']--;
}
for (int i = 0; i < 26; i++) {
if (letters[i] != 0) {
return false;
}
}
return true;
}
}
115. Distinct Subsequences
Description
Given a string S and a string T, count the number of distinct subsequences of S which equals T.
A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, “ACE” is a subsequence of “ABCDE” while “AEC” is not).
It’s guaranteed the answer fits on a 32-bit signed integer.
Example 1:
Input: S = "rabbbit", T = "rabbit"
Output: 3
Explanation:
As shown below, there are 3 ways you can generate "rabbit" from S.
(The caret symbol ^ means the chosen letters)
rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^
Example 2:
Input: S = "babgbag", T = "bag"
Output: 5
Explanation:
As shown below, there are 5 ways you can generate "bag" from S.
(The caret symbol ^ means the chosen letters)
babgbag
^^ ^
babgbag
^^ ^
babgbag
^ ^^
babgbag
^ ^^
babgbag
^^^
Solution
class Solution {
public int numDistinct(String S, String T) {
// array creation
int[][] mem = new int[T.length()+1][S.length()+1];
// filling the first row: with 1s
for(int j=0; j<=S.length(); j++) {
mem[0][j] = 1;
}
// the first column is 0 by default in every other rows but the first, which we need.
for(int i=0; i<T.length(); i++) {
for(int j=0; j<S.length(); j++) {
if(T.charAt(i) == S.charAt(j)) {
mem[i+1][j+1] = mem[i][j] + mem[i+1][j];
} else {
mem[i+1][j+1] = mem[i+1][j];
}
}
}
return mem[T.length()][S.length()];
}
}
214. Shortest Palindrome
Description
Given a string s, you are allowed to convert it to a palindrome by adding characters in front of it. Find and return the shortest palindrome you can find by performing this transformation.
Example 1:
Input: "aacecaaa"
Output: "aaacecaaa"
Example 2:
Input: "abcd"
Output: "dcbabcd"
Solution
class Solution {
public String shortestPalindrome(String s) {
StringBuilder builder = new StringBuilder();
builder.append(s);
builder = builder.reverse();
String reversedString = builder.toString();
for (int i = 0; i < s.length(); i++) {
//if s startwith reverse[i:] means the overlaped part must be a palidorm
//bcba + abcb -> bcb is overlaped
if (s.startsWith(reversedString.substring(i))) {
return reversedString.substring(0, i) + s;
}
}
return reversedString + s;
}
}
541. Reverse String II
Description
Given a string and an integer k, you need to reverse the first k characters for every 2k characters counting from the start of the string. If there are less than k characters left, reverse all of them. If there are less than 2k but greater than or equal to k characters, then reverse the first k characters and left the other as original.
Example:
Input: s = "abcdefg", k = 2
Output: "bacdfeg"
Restrictions:
The string consists of lower English letters only.
Length of the given string and k will in the range [1, 10000]
Solution
class Solution {
public String reverseStr(String s, int k) {
char[] arr = s.toCharArray();
int n = arr.length;
int i = 0;
while (i < n) {
int j = Math.min(i + k - 1, n - 1);
swap(arr, i, j);
i += 2 * k;
}
return String.valueOf(arr);
}
private void swap(char[] arr, int l, int r) {
while (l < r) {
char temp = arr[l];
arr[l++] = arr[r];
arr[r--] = temp;
}
}
}
2020-06-30
58. Length of Last Word
Description
Given a string s consists of upper/lower-case alphabets and empty space characters ‘ ‘, return the length of last word (last word means the last appearing word if we loop from left to right) in the string.
If the last word does not exist, return 0.
Note: A word is defined as a maximal substring consisting of non-space characters only.
Example:
Input: "Hello World"
Output: 5
Solution
class Solution {
public int lengthOfLastWord(String s) {
int i = s.length() - 1;
int len = 0;
while (i >= 0) {
if (s.charAt(i) != ' ') {
break;
}
i--;
}
while (i >= 0 && s.charAt(i) != ' ') {
len++;
i--;
}
return len;
}
}
681. Next Closest Time
Description
Given a time represented in the format “HH:MM”, form the next closest time by reusing the current digits. There is no limit on how many times a digit can be reused.
You may assume the given input string is always valid. For example, “01:34”, “12:09” are all valid. “1:34”, “12:9” are all invalid.
Example 1:
Input: "19:34"
Output: "19:39"
Explanation: The next closest time choosing from digits 1, 9, 3, 4, is 19:39, which occurs 5 minutes later. It is not 19:33, because this occurs 23 hours and 59 minutes later.
Example 2:
Input: "23:59"
Output: "22:22"
Explanation: The next closest time choosing from digits 2, 3, 5, 9, is 22:22. It may be assumed that the returned time is next day's time since it is smaller than the input time numerically.
Solution
/**
Jump to next time and check if it's valid.
*/
class Solution {
public String nextClosestTime(String time) {
String[] clock = time.split(":");
int hour = Integer.parseInt(clock[0]);
int minute = Integer.parseInt(clock[1]);
HashSet<Integer> used = new HashSet<>();
for (int i = 0; i < time.length(); i++) {
if (!Character.isDigit(time.charAt(i))) {
continue;
}
used.add(time.charAt(i)-'0');
}
boolean flag = true;
while(true){
flag = true;
minute+=1;
if(minute==60){
minute=0;
hour+=1;
hour%=24;
}
flag &= used.contains(minute/10);
flag &= used.contains(minute%10);
if(!flag)continue;
flag &= used.contains(hour/10);
flag &= used.contains(hour%10);
if(flag){
StringBuilder sb = new StringBuilder();
sb.append(hour/10);
sb.append(hour%10);
sb.append(":");
sb.append(minute/10);
sb.append(minute%10);
return sb.toString();
}
}
}
}
686. Repeated String Match
Description
Given two strings A and B, find the minimum number of times A has to be repeated such that B is a substring of it. If no such solution, return -1.
For example, with A = "abcd" and B = "cdabcdab".
Return 3, because by repeating A three times (“abcdabcdabcd”), B is a substring of it; and B is not a substring of A repeated two times ("abcdabcd").
Note:
The length of A and B will be between 1 and 10000.
Solution
//keep building until valid.
class Solution {
public int repeatedStringMatch(String A, String B) {
int count = 0;
StringBuilder sb = new StringBuilder();
while (sb.length() < B.length()) {
sb.append(A);
count++;
}
if (sb.toString().contains(B)) {
return count;
}
if (sb.append(A).toString().contains(B)) {
return ++count;
}
return -1;
}
}
1188. Design Bounded Blocking Queue
Description
Implement a thread safe bounded blocking queue that has the following methods:
BoundedBlockingQueue(int capacity) The constructor initializes the queue with a maximum capacity.
void enqueue(int element) Adds an element to the front of the queue. If the queue is full, the calling thread is blocked until the queue is no longer full.
int dequeue() Returns the element at the rear of the queue and removes it. If the queue is empty, the calling thread is blocked until the queue is no longer empty.
int size() Returns the number of elements currently in the queue.
Your implementation will be tested using multiple threads at the same time. Each thread will either be a producer thread that only makes calls to the enqueue method or a consumer thread that only makes calls to the dequeue method. The size method will be called after every test case.
Please do not use built-in implementations of bounded blocking queue as this will not be accepted in an interview.
Example 1:
Input:
1
1
["BoundedBlockingQueue","enqueue","dequeue","dequeue","enqueue","enqueue","enqueue","enqueue","dequeue"]
[[2],[1],[],[],[0],[2],[3],[4],[]]
Output:
[1,0,2,2]
Explanation:
Number of producer threads = 1
Number of consumer threads = 1
BoundedBlockingQueue queue = new BoundedBlockingQueue(2); // initialize the queue with capacity = 2.
queue.enqueue(1); // The producer thread enqueues 1 to the queue.
queue.dequeue(); // The consumer thread calls dequeue and returns 1 from the queue.
queue.dequeue(); // Since the queue is empty, the consumer thread is blocked.
queue.enqueue(0); // The producer thread enqueues 0 to the queue. The consumer thread is unblocked and returns 0 from the queue.
queue.enqueue(2); // The producer thread enqueues 2 to the queue.
queue.enqueue(3); // The producer thread enqueues 3 to the queue.
queue.enqueue(4); // The producer thread is blocked because the queue's capacity (2) is reached.
queue.dequeue(); // The consumer thread returns 2 from the queue. The producer thread is unblocked and enqueues 4 to the queue.
queue.size(); // 2 elements remaining in the queue. size() is always called at the end of each test case.
Example 2:
Input:
3
4
["BoundedBlockingQueue","enqueue","enqueue","enqueue","dequeue","dequeue","dequeue","enqueue"]
[[3],[1],[0],[2],[],[],[],[3]]
Output:
[1,0,2,1]
Explanation:
Number of producer threads = 3
Number of consumer threads = 4
BoundedBlockingQueue queue = new BoundedBlockingQueue(3); // initialize the queue with capacity = 3.
queue.enqueue(1); // Producer thread P1 enqueues 1 to the queue.
queue.enqueue(0); // Producer thread P2 enqueues 0 to the queue.
queue.enqueue(2); // Producer thread P3 enqueues 2 to the queue.
queue.dequeue(); // Consumer thread C1 calls dequeue.
queue.dequeue(); // Consumer thread C2 calls dequeue.
queue.dequeue(); // Consumer thread C3 calls dequeue.
queue.enqueue(3); // One of the producer threads enqueues 3 to the queue.
queue.size(); // 1 element remaining in the queue.
Since the number of threads for producer/consumer is greater than 1, we do not know how the threads will be scheduled in the operating system, even though the input seems to imply the ordering. Therefore, any of the output [1,0,2] or [1,2,0] or [0,1,2] or [0,2,1] or [2,0,1] or [2,1,0] will be accepted.
Solution
/**
semaphore: acquire -1, release +1.
*/
import java.util.concurrent.ConcurrentLinkedQueue;
import java.util.concurrent.Semaphore;
class BoundedBlockingQueue {
private Semaphore enq;
private Semaphore deq;
ConcurrentLinkedQueue<Integer> queue;
public BoundedBlockingQueue(int capacity) {
queue = new ConcurrentLinkedQueue<>();
enq = new Semaphore(capacity);
deq = new Semaphore(0);
}
public void enqueue(int element) throws InterruptedException {
enq.acquire();
queue.offer(element);
deq.release();
}
public int dequeue() throws InterruptedException {
deq.acquire();
int res = queue.poll();
enq.release();
return res;
}
public int size() {
return queue.size();
}
}