- 2020-08-24
- 2020-08-25
- 2020-08-26
2020-08-24
1359. Count All Valid Pickup and Delivery Options
Description
Given n orders, each order consist in pickup and delivery services.
Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).
Since the answer may be too large, return it modulo 10^9 + 7.
Example 1:
Input: n = 1
Output: 1
Explanation: Unique order (P1, D1), Delivery 1 always is after of Pickup 1.
Example 2:
Input: n = 2
Output: 6
Explanation: All possible orders:
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.
Example 3:
Input: n = 3
Output: 90
Constraints:
1 <= n <= 500
Solution
/**
n=2 -> (4)1 (3)1 (2)1(1) 1
(x) means theres x ways to set up the pickup, or x slots to pickup after current time.
so res = res * (i * 2 - 1) * i % mod;
*/
class Solution {
public int countOrders(int n) {
//use long to prevent overflow.
long res = 1, mod = (long)1e9 + 7;
for (int i = 1; i <= n; ++i)
res = res * (i * 2 - 1) * i % mod;
return (int)res;
}
}
1376. Time Needed to Inform All Employees
Description
A company has n employees with a unique ID for each employee from 0 to n - 1. The head of the company has is the one with headID.
Each employee has one direct manager given in the manager array where manager[i] is the direct manager of the i-th employee, manager[headID] = -1. Also it's guaranteed that the subordination relationships have a tree structure.
The head of the company wants to inform all the employees of the company of an urgent piece of news. He will inform his direct subordinates and they will inform their subordinates and so on until all employees know about the urgent news.
The i-th employee needs informTime[i] minutes to inform all of his direct subordinates (i.e After informTime[i] minutes, all his direct subordinates can start spreading the news).
Return the number of minutes needed to inform all the employees about the urgent news.
Example 1:
Input: n = 1, headID = 0, manager = [-1], informTime = [0]
Output: 0
Explanation: The head of the company is the only employee in the company.
Example 2:
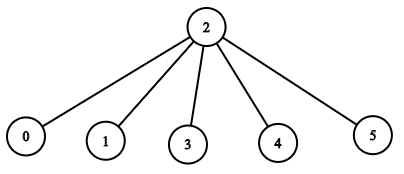
Input: n = 6, headID = 2, manager = [2,2,-1,2,2,2], informTime = [0,0,1,0,0,0]
Output: 1
Explanation: The head of the company with id = 2 is the direct manager of all the employees in the company and needs 1 minute to inform them all.
The tree structure of the employees in the company is shown.
Example 3:
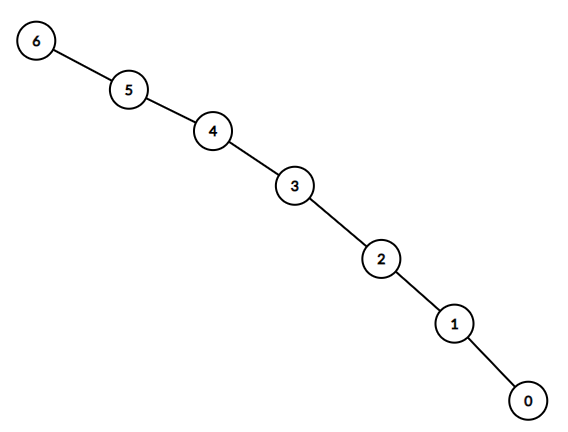
Input: n = 7, headID = 6, manager = [1,2,3,4,5,6,-1], informTime = [0,6,5,4,3,2,1]
Output: 21
Explanation: The head has id = 6. He will inform employee with id = 5 in 1 minute.
The employee with id = 5 will inform the employee with id = 4 in 2 minutes.
The employee with id = 4 will inform the employee with id = 3 in 3 minutes.
The employee with id = 3 will inform the employee with id = 2 in 4 minutes.
The employee with id = 2 will inform the employee with id = 1 in 5 minutes.
The employee with id = 1 will inform the employee with id = 0 in 6 minutes.
Needed time = 1 + 2 + 3 + 4 + 5 + 6 = 21.
Example 4:
Input: n = 15, headID = 0, manager = [-1,0,0,1,1,2,2,3,3,4,4,5,5,6,6], informTime = [1,1,1,1,1,1,1,0,0,0,0,0,0,0,0]
Output: 3
Explanation: The first minute the head will inform employees 1 and 2.
The second minute they will inform employees 3, 4, 5 and 6.
The third minute they will inform the rest of employees.
Example 5:
Input: n = 4, headID = 2, manager = [3,3,-1,2], informTime = [0,0,162,914]
Output: 1076
Constraints:
1 <= n <= 10^5
0 <= headID < n
manager.length == n
0 <= manager[i] < n
manager[headID] == -1
informTime.length == n
0 <= informTime[i] <= 1000
informTime[i] == 0 if employee i has no subordinates.
It is guaranteed that all the employees can be informed.
Solution
class Solution {
public int numOfMinutes(final int n, final int headID, final int[] manager, final int[] informTime) {
final Map<Integer, List<Integer>> graph = new HashMap<>();
int total = 0;
for (int i = 0; i < manager.length; i++) {
int j = manager[i];
if (!graph.containsKey(j)) {
graph.put(j, new ArrayList<>());
}
graph.get(j).add(i);
}
return dfs(graph, informTime, headID);
}
private int dfs(final Map<Integer, List<Integer>> graph, final int[] informTime, final int cur) {
int max = 0;
if (!graph.containsKey(cur)) {
return max;
}
for (int person : graph.get(cur)) {
max = Math.max(max, dfs(graph, informTime, person));
}
return max + informTime[cur];
}
}
1010. Pairs of Songs With Total Durations Divisible by 60
Description
In a list of songs, the i-th song has a duration of time[i] seconds.
Return the number of pairs of songs for which their total duration in seconds is divisible by 60. Formally, we want the number of indices i, j such that i < j with (time[i] + time[j]) % 60 == 0.
Example 1:
Input: [30,20,150,100,40]
Output: 3
Explanation: Three pairs have a total duration divisible by 60:
(time[0] = 30, time[2] = 150): total duration 180
(time[1] = 20, time[3] = 100): total duration 120
(time[1] = 20, time[4] = 40): total duration 60
Example 2:
Input: [60,60,60]
Output: 3
Explanation: All three pairs have a total duration of 120, which is divisible by 60.
Note:
1 <= time.length <= 60000
1 <= time[i] <= 500
Solution
class Solution {
public int numPairsDivisibleBy60(int[] time) {
int[] map =new int[60];
int res = 0;
for(int t : time){
//special case
//if t % 60 = 0, (t % 60) % 60 = 0 instead of 60.
res += map[(60 - t % 60) % 60];
map[t % 60]++;
}
return res;
}
}
1216. Valid Palindrome III
Description
Given a string s and an integer k, find out if the given string is a K-Palindrome or not.
A string is K-Palindrome if it can be transformed into a palindrome by removing at most k characters from it.
Example 1:
Input: s = "abcdeca", k = 2
Output: true
Explanation: Remove 'b' and 'e' characters.
Constraints:
1 <= s.length <= 1000
s has only lowercase English letters.
1 <= k <= s.length
Solution
/**
Find Longest Palindrom.
*/
class Solution {
public boolean isValidPalindrome(String str, int k) {
int n = str.length();
StringBuilder stringBuilder = new StringBuilder(str).reverse();
int lps = lcs(str, stringBuilder.toString(), n, n);
return (n - lps <= k);
}
/*
longest palindromic subsequence:
LCS of the given string & its reverse will be the longest palindromic sequence.
*/
private int lcs(String X, String Y, int m, int n) {
int[][] dp = new int[m + 1][n + 1];
for (int i = 1; i <= m; i++) {
for (int j = 1; j <= n; j++) {
if (X.charAt(i - 1) == Y.charAt(j - 1)) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[m][n];
}
}
1013. Partition Array Into Three Parts With Equal Sum
Description
Given an array A of integers, return true if and only if we can partition the array into three non-empty parts with equal sums.
Formally, we can partition the array if we can find indexes i+1 < j with (A[0] + A[1] + ... + A[i] == A[i+1] + A[i+2] + ... + A[j-1] == A[j] + A[j-1] + ... + A[A.length - 1])
Example 1:
Input: A = [0,2,1,-6,6,-7,9,1,2,0,1]
Output: true
Explanation: 0 + 2 + 1 = -6 + 6 - 7 + 9 + 1 = 2 + 0 + 1
Example 2:
Input: A = [0,2,1,-6,6,7,9,-1,2,0,1]
Output: false
Example 3:
Input: A = [3,3,6,5,-2,2,5,1,-9,4]
Output: true
Explanation: 3 + 3 = 6 = 5 - 2 + 2 + 5 + 1 - 9 + 4
Constraints:
3 <= A.length <= 50000
-10^4 <= A[i] <= 10^4
Solution
class Solution {
public boolean canThreePartsEqualSum(int[] A) {
int sum = 0;
for(int num:A){
sum += num;
}
if(sum % 3 !=0){
return false;
}
sum /= 3;
int i =0,tempSum = 0;
while(i < A.length){
tempSum += A[i];
if(tempSum == sum){
break;
}
i++;
}
int j = A.length-1;
tempSum = 0;
while(j>=0){
tempSum += A[j];
if(tempSum == sum){
break;
}
j--;
}
//System.out.println(i+" "+ j);
return j-i>1;
}
}
161. One Edit Distance
Description
Given two strings s and t, determine if they are both one edit distance apart.
Note:
There are 3 possiblities to satisify one edit distance apart:
Insert a character into s to get t
Delete a character from s to get t
Replace a character of s to get t
Example 1:
Input: s = "ab", t = "acb"
Output: true
Explanation: We can insert 'c' into s to get t.
Example 2:
Input: s = "cab", t = "ad"
Output: false
Explanation: We cannot get t from s by only one step.
Example 3:
Input: s = "1203", t = "1213"
Output: true
Explanation: We can replace '0' with '1' to get t.
Solution
class Solution {
public boolean isOneEditDistance(String s, String t) {
int i = 0, j = 0;
int sLen =s.length();
int tLen = t.length();
while (i < sLen && j < tLen) {
if(s.charAt(i)!=t.charAt(j)){
if(sLen==tLen){
return s.substring(i+1).equals(t.substring(j+1));
}else if(sLen<tLen){
return s.substring(i).equals(t.substring(j+1));
}else{
return s.substring(i+1).equals(t.substring(j));
}
}
i++;
j++;
}
return Math.abs(s.length() - t.length()) == 1;
}
}
316. Remove Duplicate Letters
Description
Given a string which contains only lowercase letters, remove duplicate letters so that every letter appears once and only once. You must make sure your result is the smallest in lexicographical order among all possible results.
Example 1:
Input: "bcabc"
Output: "abc"
Example 2:
Input: "cbacdcbc"
Output: "acdb"
Solution
class Solution {
public String removeDuplicateLetters(String S) {
ArrayDeque<Integer> stack = new ArrayDeque<>();
int[] last = new int[26];
boolean[] seen = new boolean[26];
for (int i = 0; i < S.length(); ++i) {
last[S.charAt(i) - 'a'] = i;
}
for (int i = 0; i < S.length(); ++i) {
int c = S.charAt(i) - 'a';
if (seen[c]) {
continue;
}
//only when the following meet can remove the previous char:
//1. the prev char is larger than cur
//2. It is not the last for that char.
while (!stack.isEmpty() && stack.peek() > c && i < last[stack.peek()]) {
//removed from stack and pretend we never met.
seen[stack.pop()] = false;
}
stack.push(c);
seen[c] = true;
}
StringBuilder sb = new StringBuilder();
while (!stack.isEmpty()) {
sb.append((char) ('a' + stack.pollLast()));
}
return sb.toString();
}
}
2020-08-25
1360. Number of Days Between Two Dates
Description
Write a program to count the number of days between two dates.
The two dates are given as strings, their format is YYYY-MM-DD as shown in the examples.
Example 1:
Input: date1 = "2019-06-29", date2 = "2019-06-30"
Output: 1
Example 2:
Input: date1 = "2020-01-15", date2 = "2019-12-31"
Output: 15
Constraints:
The given dates are valid dates between the years 1971 and 2100.
Solution
//Count the total days between current date to 1971 and then compare.
class Solution {
public int daysBetweenDates(String date1, String date2) {
return Math.abs(distTo1971(date1) - distTo1971(date2));
}
public boolean isLeap(int year) {
return (year % 400 == 0) || (year % 4 == 0 && year % 100 != 0);
}
public int distTo1971(String date) {
int[] daysInMonth = new int[]{0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
String[] dateArr = date.split("-");
if (dateArr.length != 3) {
return -1;
}
int year = Integer.parseInt(dateArr[0]);
int month = Integer.parseInt(dateArr[1]);
int day = Integer.parseInt(dateArr[2]);
for (int i = 1971; i < year; i++) {
day += isLeap(i) ? 366 : 365;
}
for (int i = 1; i < month; i++) {
day += daysInMonth[i];
if (i == 2 && isLeap(year)) {
day++;
}
}
return day;
}
}
536. Construct Binary Tree from String
Description
You need to construct a binary tree from a string consisting of parenthesis and integers.
The whole input represents a binary tree. It contains an integer followed by zero, one or two pairs of parenthesis. The integer represents the root's value and a pair of parenthesis contains a child binary tree with the same structure.
You always start to construct the left child node of the parent first if it exists.
Example:
Input: "4(2(3)(1))(6(5))"
Output: return the tree root node representing the following tree:
4
/ \
2 6
/ \ /
3 1 5
Note:
There will only be '(', ')', '-' and '0' ~ '9' in the input string.
An empty tree is represented by "" instead of "()".
Solution
//use count to find the split( left +1, right -1)
//Then use recursion to resolve a valid string to tree.
class Solution {
public TreeNode str2tree(String s) {
if (s == null || s.isEmpty() || s.charAt(0) == '(' || s.charAt(0) == ')') {
return null;
}
int index = 0;
while (index < s.length() && (s.charAt(index) != '(' && s.charAt(index) != ')')) {
index++;
}
int val = Integer.parseInt(s.substring(0, index));
TreeNode root = new TreeNode(val);
if (index == s.length()) {
return root;
}
int count = 1;
int leftIndex = index + 1;
while (leftIndex < s.length() && count != 0) {
if (s.charAt(leftIndex) == '(') {
count++;
} else if (s.charAt(leftIndex) == ')') {
count--;
}
leftIndex++;
}
root.left = str2tree(s.substring(index + 1, leftIndex - 1));
if (leftIndex != s.length()) {
root.right = str2tree(s.substring(leftIndex + 1, s.length() - 1));
}
return root;
}
}
2020-08-26
1424. Diagonal Traverse II
Description
Given a list of lists of integers, nums, return all elements of nums in diagonal order as shown in the below images.
Example 1:
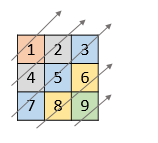
Input: nums = [[1,2,3],[4,5,6],[7,8,9]]
Output: [1,4,2,7,5,3,8,6,9]
Example 2:
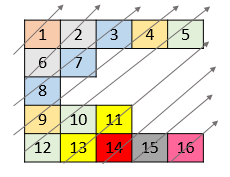
Input: nums = [[1,2,3,4,5],[6,7],[8],[9,10,11],[12,13,14,15,16]]
Output: [1,6,2,8,7,3,9,4,12,10,5,13,11,14,15,16]
Example 3:
Input: nums = [[1,2,3],[4],[5,6,7],[8],[9,10,11]]
Output: [1,4,2,5,3,8,6,9,7,10,11]
Example 4:
Input: nums = [[1,2,3,4,5,6]]
Output: [1,2,3,4,5,6]
Constraints:
1 <= nums.length <= 10^5
1 <= nums[i].length <= 10^5
1 <= nums[i][j] <= 10^9
There at most 10^5 elements in nums.
Solution
/**
Use map to store same dialog.
*/
class Solution {
public int[] findDiagonalOrder(List<List<Integer>> nums) {
HashMap<Integer, List<Integer>> map = new HashMap<>();
int max = 0;
for (int i = 0; i < nums.size(); i++) {
List<Integer> list = nums.get(i);
for (int j = 0; j < list.size(); j++) {
map.putIfAbsent(i+j,new ArrayList<>());
map.get(i+j).add(0,list.get(j));
max = Math.max(max,i+j);
}
}
List<Integer> res = new ArrayList<>();
for(int i = 0;i<=max;i++){
res.addAll(map.getOrDefault(i,new ArrayList<>()));
}
return res.stream().mapToInt(i->i).toArray();
}
}
1246. Palindrome Removal
Description
Given an integer array arr, in one move you can select a palindromic subarray arr[i], arr[i+1], ..., arr[j] where i <= j, and remove that subarray from the given array. Note that after removing a subarray, the elements on the left and on the right of that subarray move to fill the gap left by the removal.
Return the minimum number of moves needed to remove all numbers from the array.
Example 1:
Input: arr = [1,2]
Output: 2
Example 2:
Input: arr = [1,3,4,1,5]
Output: 3
Explanation: Remove [4] then remove [1,3,1] then remove [5].
Constraints:
1 <= arr.length <= 100
1 <= arr[i] <= 20
Solution
/**
We can solve this problem using Dynamic programming. Let dp[i][j] denotes the number of steps it takes to delete the substring s[i, j]. Each character will be deleted alone or as part of some substring so in the first case we will delete the character itself and call subproblem (i+1, j). In the second case we will iterate over all occurrence of the current character in right side, if K is the index of one such occurrence then the problem will reduce to two subproblems (i+1, K – 1) and (K+1, j). We can reach to this subproblem (i+1, K-1) because we can just delete the same character and call for mid substring. We need to take care of a case when first two characters are same in that case we can directly reduce to the subproblem (i+2, j)
So after above discussion of relation among subproblems, we can write dp relation as follows,
dp[i][j] = min(1 + dp[i+1][j],
dp[i+1][K-1] + dp[K+1][j], where s[i] == s[K]
1 + dp[i+2][j] )
Total time complexity of above solution is O(n^3)
*/
class Solution {
int[][] dp;
public int minimumMoves(int[] arr) {
dp = new int[arr.length][arr.length];
return dfs(arr, 0, arr.length - 1);
}
private int dfs(int[] arr, int i, int j) {
if (i >= j) {
return i == j ? 1 : 0;
}
if (dp[i][j] > 0) {
return dp[i][j];
}
int res = dfs(arr, i + 1, j) + 1;
if (i + 1 < arr.length && arr[i] == arr[i + 1]) {
res = Math.min(res, dfs(arr, i + 2, j) + 1);
}
for (int k = i + 2; k <= j; k++) {
if (arr[i] == arr[k]) {
res = Math.min(res, dfs(arr, i + 1, k - 1) + dfs(arr, k + 1, j));
}
}
dp[i][j] = res;
return res;
}
}